e# Distribuição normal
Introdução
A curva de densidade, também conhecida como função de densidade de probabilidade ou PDF (Probability Density Function), é uma representação gráfica que descreve a distribuição de probabilidade de uma variável contínua. Ela é frequentemente usada em estatísticas e análise de dados para visualizar a forma da distribuição de uma variável contínua e entender sua tendência central, dispersão e outros padrões.
A curva de densidade é uma forma suavizada da distribuição de probabilidade, que é uma descrição completa das probabilidades de diferentes valores de uma variável. A curva de densidade não fornece probabilidades diretas como a distribuição de probabilidade, mas mostra como a probabilidade é distribuída ao longo do intervalo de valores possíveis.
As características da curva de densidade podem variar com base na distribuição subjacente da variável, ou seja, o formato da curva está relacionado ao tipo de distribuição de probabilidade que melhor se ajusta aos valores observados da variável. Algumas distribuições comuns incluem a distribuição normal (gaussiana), a distribuição exponencial, a distribuição uniforme, entre outras. Isso é importante porque muitos métodos estatísticos e de análise pressupõem uma certa distribuição subjacente para funcionar corretamente.
A forma da curva de densidade pode ser simétrica ou assimétrica, ter picos únicos ou múltiplos, e apresentar diferentes graus de dispersão, como é possível visualizar nas figuras abaixo:
-
Curva de densidade simétrica:
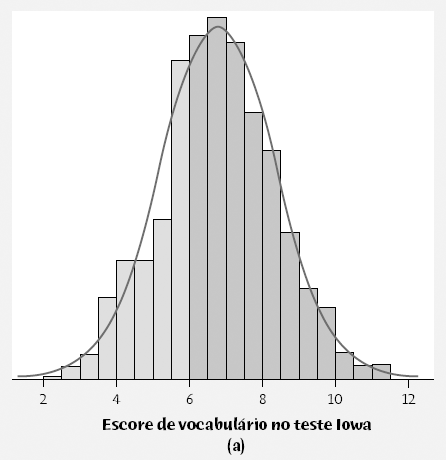
-
Curva de densidade simétrica:
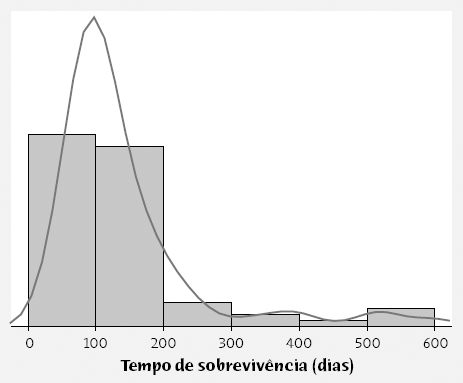
A área sob a curva de densidade ao longo de um intervalo específico representa a probabilidade de a variável cair nesse intervalo. Ou seja, a área total sob a curva de densidade é igual a 1, indicando que os valores possíveis da variável estão totalmente cobertos pelas probabilidades.
A curva de densidade é uma ferramenta fundamental para entender as propriedades estatísticas de uma variável contínua, identificar padrões, detectar anomalias e tomar decisões informadas com base na distribuição dos dados.
Descrição das curvas de densidade
A descrição das curvas de densidade é uma abordagem para compreender as propriedades estatísticas das distribuições de dados por meio de representações gráficas contínuas, chamadas curvas de densidade. Essas curvas oferecem uma visão mais suave e idealizada das distribuições subjacentes, permitindo analisar características como média, mediana e outras propriedades.
Mediana e quartis:
Na análise das curvas de densidade, a mediana e os quartis têm interpretações semelhantes às observações reais. A mediana é o ponto que divide a área sob a curva em partes iguais, ou seja, metade das observações estão à esquerda e metade à direita desse ponto. Os quartis dividem a área sob a curva em quartos, indicando onde estão localizados os 25%, 50% e 75% dos dados.

No entanto, em curvas assimétricas, a média é puxada em direção à cauda longa da distribuição.
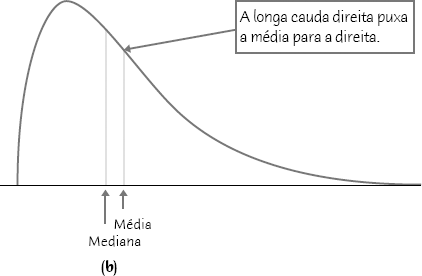
Diferença entre média e desvio-padrão da curva de densidade e das observações reais:
É importante fazer a distinção entre a média () e o desvio-padrão () de uma curva de densidade e a média () e o desvio-padrão () calculados a partir das observações reais. Enquanto a média () da curva de densidade é um ponto de equilíbrio idealizado, a média () das observações reais é uma média aritmética. O desvio-padrão () da curva de densidade descreve a dispersão dos dados ideais, seguindo a distribuição normal, enquanto o desvio-padrão () das observações reais é uma medida da dispersão dos dados reais.
Localização da média e do desvio-padrão:
A média () de uma curva de densidade pode ser localizada visualmente como o ponto de equilíbrio da curva. No entanto, não há uma maneira fácil de localizar o desvio-padrão () a olho para curvas de densidade.
Distribuições normais
Uma das principais classes de curvas de densidade são as curvas Normais que descrevem as distribuições normais. Esse tipo de distribuição possuem grande relevância na estatística, uma vez que muitos modelos matemáticos presumem que o conjunto de dados seguem a distribuição normal. Embora várias técnicas a utilizem como base, em casos reais raramente uma base de dados seguirá essa distribuição, sem que haja o tratamento do mesmo.
A identificação visual de uma distribuição normal é relativamente fácil, pois a curva Normal apresenta um formato bem peculiar, uma curva simétrica em relação a média e na forma de sino:
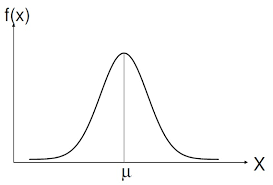
Além do formato, as curvas Normais ilustram outras propriedades relevantes, tais como:
- A curva é completamente caracterizada por sua média e seu desvio-padrão .
- A média e mediana coincidem no centro da curva simétrica
- Ao alterar a média , mas deixando o desvio-padrão inalterado, a curva Normal desloca-se ao longo do eixo horizontal (“achatando a curva”) sem modificar a dispersão.
- O desvio-padrão está relacionada à dispersão de um curva Normal, ou seja, quanto maior o desvio-padrão, menor a área sob a curva em torno da média .