Matriz de adjacência §

---

A ideia por trás da matriz de adjacência é usar uma matriz (uma tabela ou grade) quadrada, onde o número de linhas e colunas é igual ao número de vértices do grafo.

Definição §

Para um grafo , a matriz de adjacência de dimensão é definida da seguinte forma:

• O elemento da matriz é se existe uma aresta conectando o vértice e o vértice .
• O elemento é se não existe uma aresta entre eles.

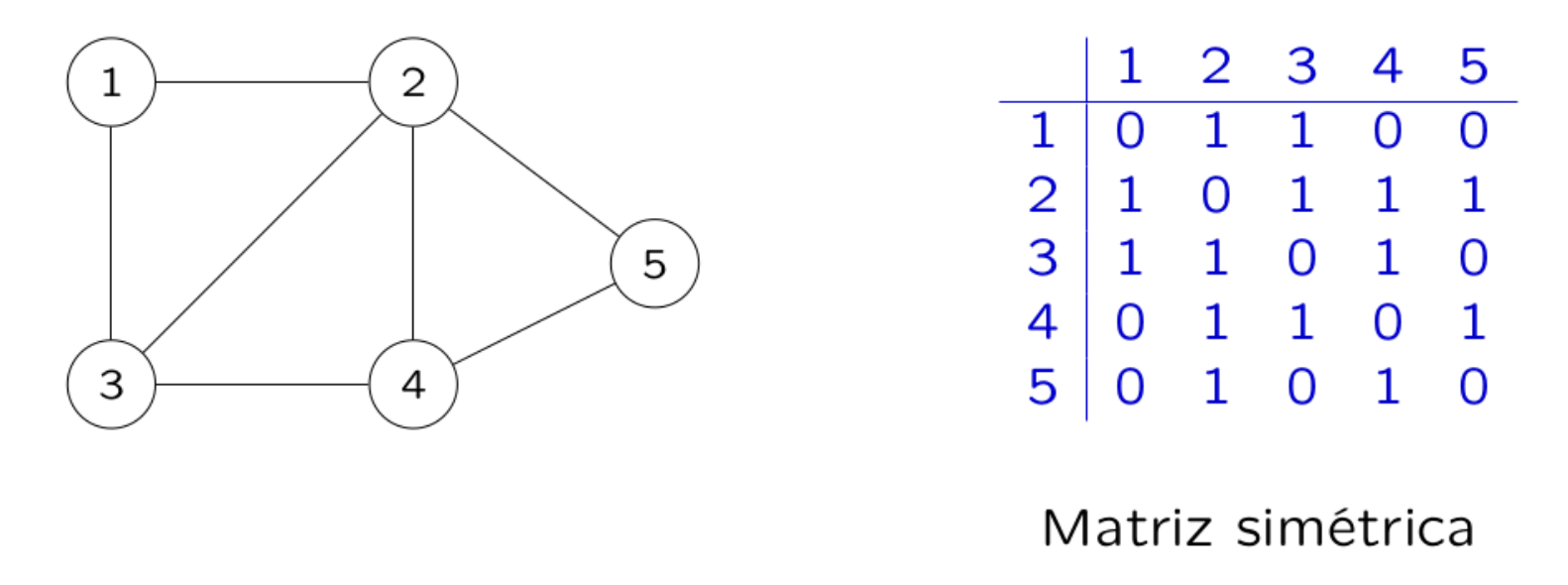
Exemplo §

Para o grafo de 5 vértices, é criada uma matriz .

Note

Uma característica importante para Grafos não direcionados é que a matriz é simétrica, ou seja, ela é igual a sua transposta.

Análise §

Vantagem: É muito rápido verificar se dois vértices são vizinhos. A busca leva tempo constante pois a estrutura de vetor garante essa eficiente no acesso de qualquer elemento pelo seus índices.

Desvantagem: o uso de memória é de , o que pode ser muito ineficiente para grafos com muitos vértices e poucas arestas (grafos esparsos).

Referências §

---

Teoria dos grafos - Representação de grafos