Teorema de aperto de mãos §

---

Para qualquer grafo , a soma dos graus de todos os seus vértices é igual ao dobro do número total de arestas.

Formalmente a fórmula é:

A prova do teorema, baseia-se em uma contagem simples:

• Ao somar os graus de todos os vértices, estamos contando quantas arestas incidem em cada vértice do grafo.
• Como cada aresta, por definição, conecta um par de vértices, ela contribui com 1 para o grau de cada um desses dois vértices.
• Portanto, cada aresta é contada exatamente duas vezes nessa soma total.

Exemplo:

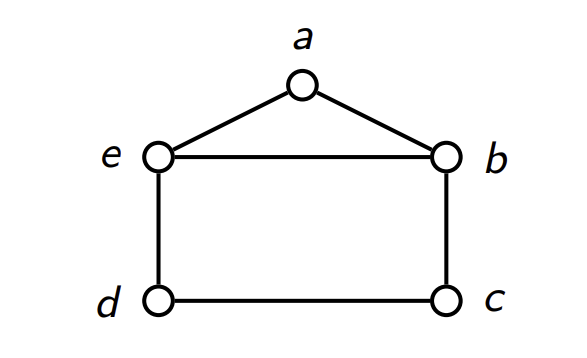
Os graus dos vértices são: , , , , e

A soma dos graus é:

Pelo teorema. sabemos que:

Corolário §

Em qualquer grafo, o número de vértices que possuem grau ímpar é sempre par.

Isso acontece porque a soma total dos graus deve ser um número par (já que é ), e a única forma de obter um número par somando uma sequência de números pares e ímpares é se houver uma quantidade par de números ímpares na soma.

Referências §

---

Teoria dos grafos - Conceitos iniciais