Valor esperado e Variância

---

O valor esperado, muitas vezes denotado como $E[X]$, é uma medida estatística que representa o centro ou a média de uma distribuição de variáveis aleatórias. Ele fornece uma estimativa de onde a maioria dos valores dessa distribuição está localizada.

Valor esperado para variáveis discretas

Para variáveis discretas, o valor esperado é calculado somando-se o produto de cada valor possível ($x_i$) pela probabilidade de ocorrência desse valor ($P(x_i)$). Isso é representado pela fórmula:

$$E[X]=\sum _{i=1}^n{x}_i\cdot P(x_i)$$

Exemplo

Seja $X$ a variável discreta randômica que tem valores 1, 2, 4, 8, 16 e uma probabilidade $P=\frac{1}{5}$. Qual é o valor esperado? $E[X]=\sum x_i\cdot P(x_i)=1\cdot \frac{1}{5}+2\cdot \frac{1}{5}+4\cdot \frac{1}{5}+8\cdot \frac{1}{5}+16\cdot \frac{1}{5}=62$

Note

Quando a probabilidade das variáveis discretas são iguais, então a fórmula do valor esperado $E[X]$ converge na fórmula da média ponderada.

No exemplo dado, o valor esperado de uma variável discreta foi calculado com base em valores específicos e suas respectivas probabilidades.

Valor esperado para variáveis contínuas

Para variáveis contínuas, o valor esperado é calculado através de uma integral que considera a multiplicação do valor ($x$) pela função de densidade de probabilidade ($f(x)$) ao longo de todo o espaço de valores possíveis:

$$E[X]={\int }_{-\infty }^{\infty }x\cdot f(x)\cdot dx$$

Exemplo

Valor esperado da variável randômica uniformemente distribuída $X$ no intervalo 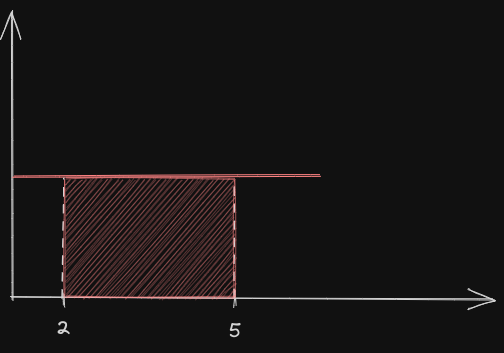$[2,5]$. Nesse exemplo, a variável $X$ é uniformemente distribuída no intervalo $[2,5]$, o que significa que todos os valores dentro desse intervalo têm a mesma probabilidade de ocorrência. No entanto, para calcular o valor esperado, é necessário ajustar a altura da função de densidade de probabilidade $f(x)$ de forma que a área total sob a curva seja igual a 1, que representa a probabilidade total.

No início, a altura do retângulo é definida como 1, pois a área total sob a curva de $f(x)$ deve ser igual a 1 de acordo com a definição de uma distribuição de probabilidade válida. No entanto, ao calcular a área do retângulo com essa altura, obtemos 3, o que não reflete corretamente a probabilidade real dentro do intervalo.

Portanto, para corrigir isso, a altura do retângulo é ajustada para $\frac{1}{3}$, de modo que a área do retângulo agora seja igual a 1, o que é consistente com a probabilidade total de 1 para esse intervalo.

Assim, o valor esperado é calculado levando em consideração essa função de densidade de probabilidade ajustada. Esse exemplo ilustra como o valor esperado é calculado em um cenário de variável contínua com uma função de densidade de probabilidade específica.

Variância

A variância, denotada como $VAR(X)$, é uma medida que quantifica a dispersão ou a variabilidade dos valores em uma distribuição de variáveis aleatórias. Ela indica o quão espalhados estão os valores em relação ao valor esperado.

O cálculo da variância é feito subtraindo o valor esperado dos quadrados dos valores individuais:

$$VAR(X)=E[(x-E[x]{)}^2]=E[x^2]-(E[x]{)}^2$$

Note

A demonstração da fórmula acima está feita na seguinte anotação: Cálculo da variância a partir do valor esperado

A variância mede o quão os valores se afastam da média. Quanto maior a variância, mais espalhados os valores estão em relação ao valor esperado.

Portanto, o valor esperado fornece uma medida central da distribuição, enquanto a variância fornece uma medida da dispersão ou propagação dos valores dessa distribuição. Ambas as medidas são essenciais na análise estatística para entender as características de um conjunto de dados.

Referências

---