Distribuição exponencial

---

Diz-se que uma variável aleatória contínua tem distribuição exponencial com parâmetro $\lambda$ se sua função de densidade de probabilidade é dada por:

$$f(x)=\{\begin{array}{l}\lambda \cdot e^{-\lambda \cdot x},x\ge 0\\ 0,x<0\end{array}$$

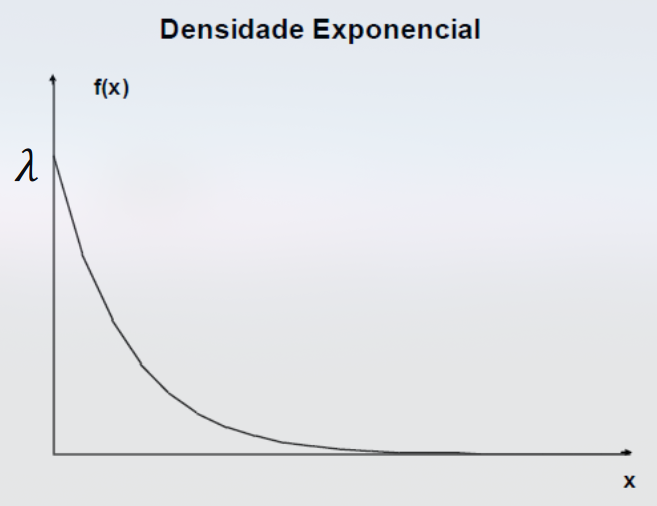
Para calcular probabilidades com a distribuição exponencial, é necessário utilizar integral, pois se trata de figuras geométricas complexas. Para isso, podemos utilizar a seguinte fórmula:

$$P(a<x<b)=e^{-\lambda a}-e^{-\lambda b}$$

Para a função de densidade acumulada, podemos simplificar a fórmula acima, uma vez que o início do intervalo ($a$) inicia-se em 0, então temos:

$$P(a<x<b)=e^{-\lambda 0}-e^{-\lambda b}=1-e^{-\lambda b}$$

Na distribuição exponencial, a esperança (média) pode ser descrita pela seguinte fórmula:

$$E(x)=\frac{1}{\lambda }$$

Já a variância pode ser calculada com:

$$var(x)=\frac{1}{{\lambda }^2}$$

Referências

---

Aula 4 – Distribuição de Probabilidades –Modelos Contínuos