introduction

Introdução ao algoritmo de Regressão Logística §

A regressão logística é um algoritmo de aprendizado supervisionado utilizado para tarefas de classificação binária e, em algumas variações, também para classificação multiclasse. Apesar do nome, a regressão logística é utilizada para prever a probabilidade de um exemplo pertencer a uma classe específica, não para realizar regressão no sentido de prever um valor numérico contínuo. A saída da regressão logística é uma probabilidade que é transformada em uma classe por meio de um limite (threshold).

A regressão logística é especialmente útil quando se trata de relacionar um conjunto de variáveis de entrada (recursos ou atributos) a uma variável de saída binária (classe), onde a saída é uma das duas classes possíveis, por exemplo, sim ou não, positivo ou negativo, etc.

O algoritmo da regressão logística utiliza a função logística (também conhecida como sigmoid) para modelar a probabilidade de um exemplo pertencer à classe positiva:

Nessa equação:

• é a probabilidade do exemplo pertencer à classe positiva, dado o conjunto de características .

• são as características (atributos) do exemplo.

• são os coeficientes que a regressão logística aprende durante o treinamento.

A regressão logística busca otimizar os coeficientes de forma a maximizar a verossimilhança dos dados observados. Isso geralmente é feito utilizando técnicas de otimização, como o método dos mínimos quadrados ou o método de gradiente descendente.

Uma vez que os coeficientes são determinados, é possível utilizar a função sigmoid para calcular as probabilidades de classe para novos exemplos e tomar uma decisão de classificação com base em um limite (threshold) definido.

Veja abaixo um exemplo no formato de gráfico o resultado da regressão logística aplicado a um conjunto de dados com o atributo “Idade” e classe “Pagar” o qual pode assumir um valor binário “S” ou “N”:

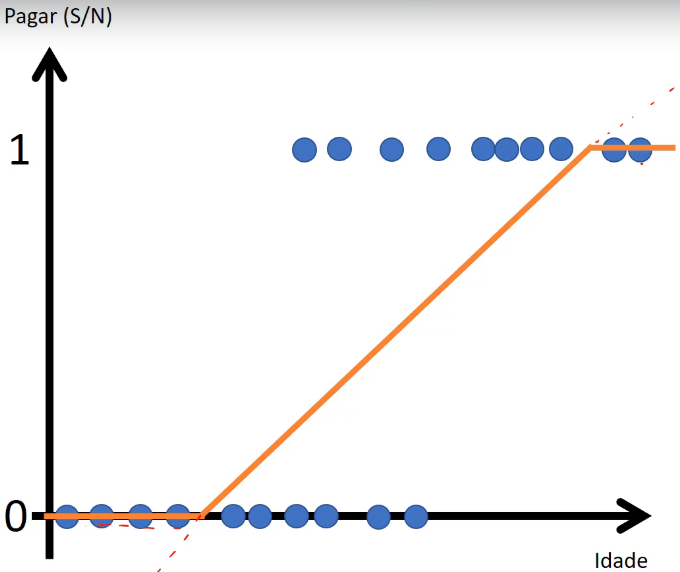
Note que a função sigmoide gera um desenho em formato de “S” (de Sigmoide)

Vantagens: §

• Relativamente simples de entender e implementar.

• Pode ser interpretado como a probabilidade de pertencer a uma classe.

• Funciona bem para problemas de classificação binária e pode ser estendido para classificação multiclasse.

Limitações: §

• Assume uma relação linear entre os atributos e o log-odds da classe.

• Pode não funcionar bem para conjuntos de dados complexos ou com relações não-lineares.

• Sensível a outliers.

Casos de uso §

• Problemas de classificação binária ou multiclasse.

• Quando se deseja entender a probabilidade de pertencer a uma classe específica.

• Como um ponto de partida inicial antes de tentar algoritmos mais complexos.

É importante notar que, embora o nome “regressão” esteja presente, a regressão logística é um algoritmo de classificação e não de regressão no sentido tradicional.