linear-and-non-linear-problems

Problemas linear e não linear §

Para compreender como o hiperplano com a máxima margem é definido, é essencial distinguir entre problemas linearmente e não linearmente separáveis.

Problema Linearmente Separável §

Considere o gráfico que representa a relação do operador lógico and (“e”):

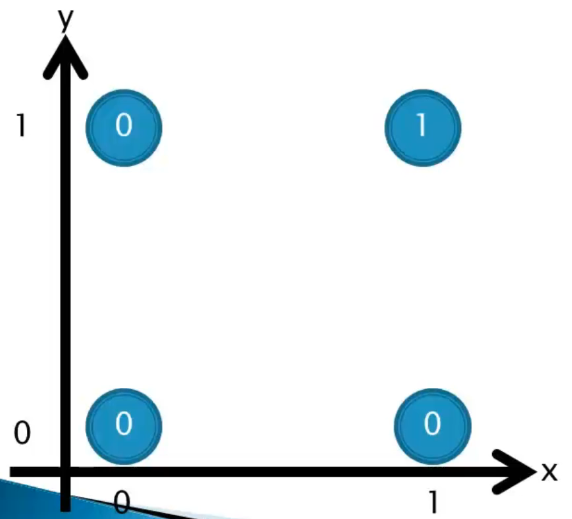
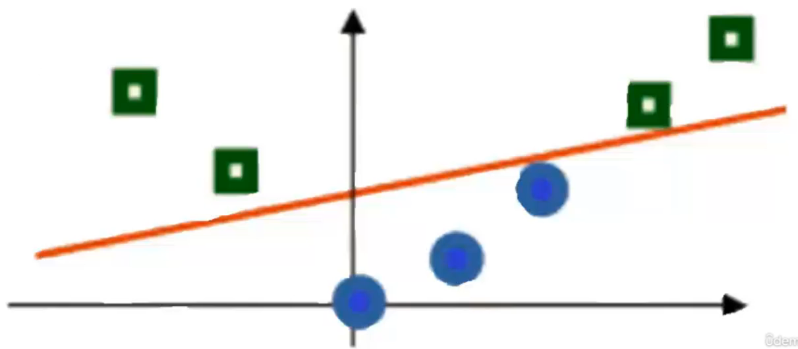
Neste cenário, podemos identificar um problema linearmente separável. É possível traçar uma reta que claramente divide as duas classes (0 e 1), tornando a separação direta.

Problema Não Linearmente Separável §

Agora, observe o gráfico que representa a relação do operador lógico xor (“ou exclusivo”):

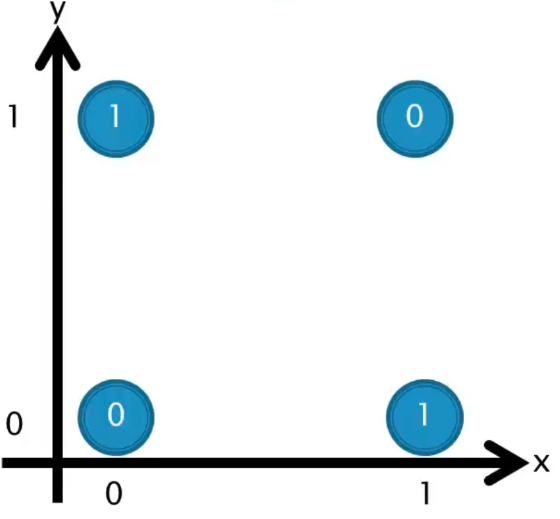
Aqui, estamos lidando com um problema não linearmente separável, pois não é viável traçar uma única reta para separar as duas classes (0 e 1).

Para abordar esse tipo de desafio, surge a técnica do kernel trick nos algoritmos SVM. Essa abordagem envolve a transformação dos dados por meio de uma função kernel, permitindo a criação de um hiperplano em um espaço de dimensões mais elevadas, onde a separação das classes seja possível. Veja a representação abaixo:

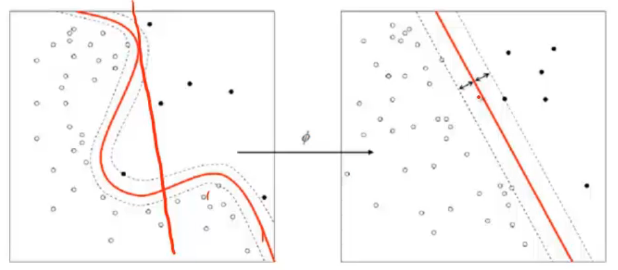
Um exemplo simples de kernel é o linear, que adiciona uma dimensão extra ao elevar os dados ao quadrado. Isso pode ser visualizado na seguinte ilustração:

Antes do Kernel Trick:

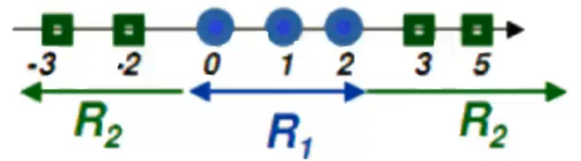
Após a aplicação da função kernel, os dados são representados da seguinte forma:

Nesse contexto:

• No eixo , temos os dados originais;
• No eixo , temos os dados elevados ao quadrado.

Funções de Kernel §

As funções de kernel são cruciais para implementar o kernel trick e tornar a separação de classes não linear possível. Algumas funções de kernel comuns incluem:

Kernel	Inner Product Kernel
Linear
Gaussiana
Polinomial
Tangente Hiperbólica

Essas funções de kernel permitem a transformação dos dados em um espaço onde as classes podem ser separadas linear ou não linearmente, abrindo caminho para uma modelagem mais flexível e precisa por parte do SVM.