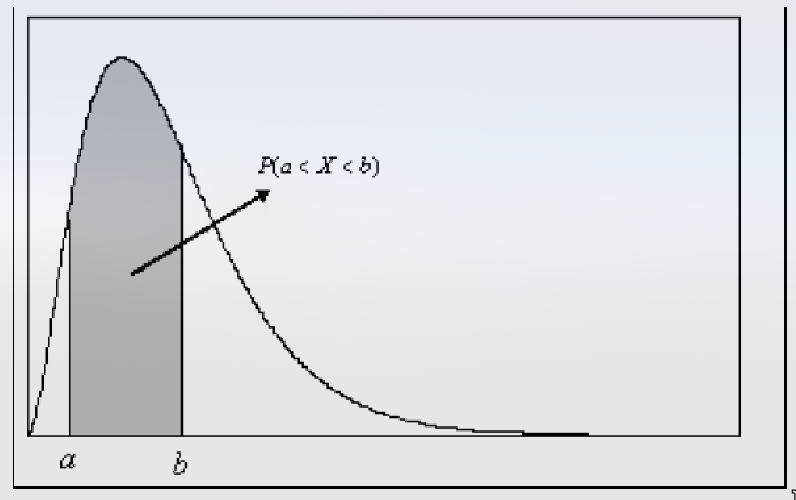
Função de densidade de probabilidade §

---

Para Variáveis aleatórias contínuas, não faz sentido falar em probabilidade de um único valor específico, pois a probabilidade de uma variável contínua assumir exatamente um valor específico é sempre zero. Em vez disso, utilizamos a função de densidade de probabilidade , que descreve a “densidade” da probabilidade ao longo do intervalo de possíveis valores.

Em outras palavras, como os valores de uma variável aleatória contínua vêm de um espaço amostral contínuo, o interesse se volta para a probabilidade de a variável assumir valores em intervalos, utilizando a função de densidade de probabilidade para descrever essa distribuição

Uma função de densidade de probabilidade é uma função que satisfaz as seguintes propriedades:

• A área total sob o gráfico de é igual a 1

Dada uma função satisfazendo as propriedades acima, então representa alguma variável contínua aleatória , de modo que é a área sob a curva entre os pontos e .

Referências §

---

Aula 4 – Distribuição de Probabilidades –Modelos Contínuos