Covariância, coeficiente de correlação e determinação
A covariância, o coeficiente de correlação e o coeficiente de determinação são conceitos estatísticos relacionados que descrevem a relação entre duas variáveis. Vamos entender cada um deles:
-
Covariância:
A covariância mede o grau de interdependência entre duas variáveis. Ela indica se as duas variáveis tendem a aumentar ou diminuir juntas. A fórmula para calcular a covariância entre duas variáveis, X e Y, em um conjunto de dados é a seguinte:
Onde:
- é o número de observações.
- e são os valores das variáveis X e Y para a i-ésima observação.
- e são as médias das variáveis X e Y, respectivamente.
A covariância pode ser positiva, negativa ou zero.
- Positiva: Isso significa que quando uma variável aumenta, a outra também tende a aumentar.
- Negativa: Quando uma variável aumenta, a outra tende a diminuir.
- Zero: Não há relação linear aparente entre as variáveis, ou seja, são independentes.
-
Coeficiente de Correlação (Correlação):
O coeficiente de correlação é uma medida padronizada que quantifica a força e a direção da relação linear entre duas variáveis. O coeficiente de correlação mais comum é o coeficiente de correlação de Pearson (r). O valor de r varia entre -1 e 1, onde:
- r = 1 indica uma correlação positiva perfeita (à medida que X aumenta, Y aumenta linearmente).
- r = -1 indica uma correlação negativa perfeita (à medida que X aumenta, Y diminui linearmente).
- r = 0 indica que não há correlação linear entre as variáveis.
A fórmula para calcular o coeficiente de correlação de Pearson é:
Onde:
- e são os desvios padrão das variáveis X e Y, respectivamente.
A tabela a seguir mostra a interpretação do coeficiente de correção:
Correlação Interpretação 0.00 a 0.19 ou 0.00 a -0.19 Correlação bem fraca 0.20 a 0.39 ou -0.20 a -0.39 Correlação fraca 0.40 a 0.69 ou -0.40 a -0.69 Correlação moderada 0.70 a 0.89 ou -0.70 a -0.89 Correlação forte 0.90 a 1.00 ou -0.90 a -1.00 Correlação muito forte -
Coeficiente de Determinação (R-squared):
O coeficiente de determinação, comumente representado como , é uma medida que indica a proporção da variabilidade total em uma variável dependente (Y) que é explicada pelas variáveis independentes (X) em um modelo de regressão linear. Em outras palavras, ele mede o quanto o modelo se ajusta aos dados.
O varia entre 0 e 1, onde:
- indica que o modelo não explica nenhuma variação na variável dependente.
- indica que o modelo explica toda a variação na variável dependente.
O é calculado como o quadrado do coeficiente de correlação de Pearson (r), o que significa que ele representa a proporção da variabilidade em Y que é compartilhada com X.
Um valor elevado de (próximo a 1) indica que o modelo de regressão linear se ajusta bem aos dados, enquanto um valor baixo (próximo a 0) sugere que o modelo não é adequado para explicar a variabilidade em Y com base em X.
Em resumo, a covariância mede a relação linear bruta entre duas variáveis, o coeficiente de correlação quantifica essa relação em uma escala padronizada, e o coeficiente de determinação indica o quão bem um modelo se ajusta aos dados, expresso como a proporção da variabilidade explicada. Essas medidas são fundamentais para entender as relações entre variáveis em análises estatísticas e de regressão.
Vale lembrar que a correlação não é causa, ou seja, mesmo que duas variáveis estejam correlacionadas isso não quer dizer que não necessariamente uma é a causa da outra e vice versa. Veja a figura abaixo:
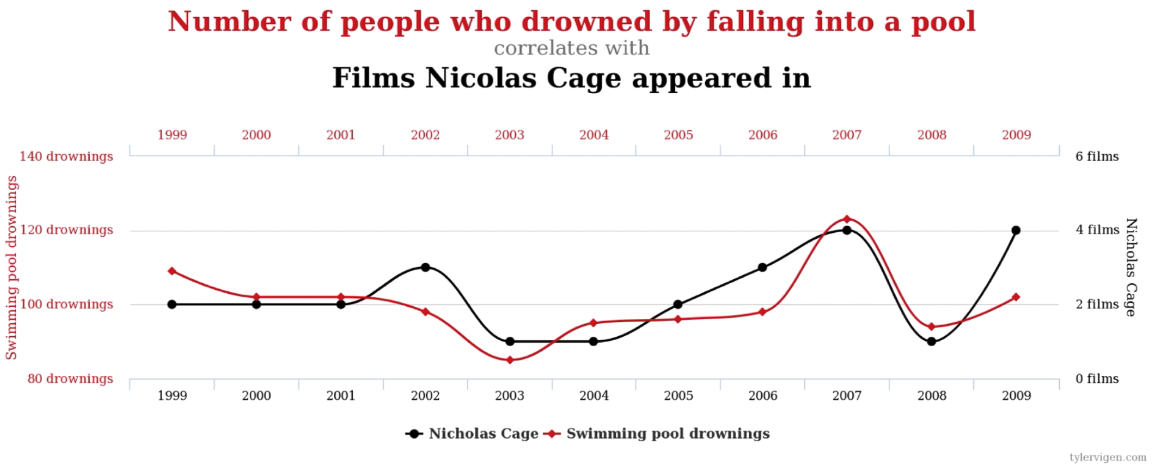
Nesse exemplo, mesmo que as variáveis “afogamento em piscina” e “aparição do Nicolas Cage nos filmes” estejam correlacionados, o número de afogamento em piscina não é explicado pelo número de filmes com a aparição de Nicolas Cade. Dessa forma, é importante realizar uma análise criteriosa antes de tirar alguma conclusão desse tipo.