Autômatos finitos

Abstract

Um autômato finito é uma máquina de estados, que permite transições de estados através da leitura de símbolos (definidos em um alfabeto) de uma entrada.

De forma geral, um autômato finito são um conjunto de regras formados por funções parciais discretas e cada função é responsável pela mudança de entrada.

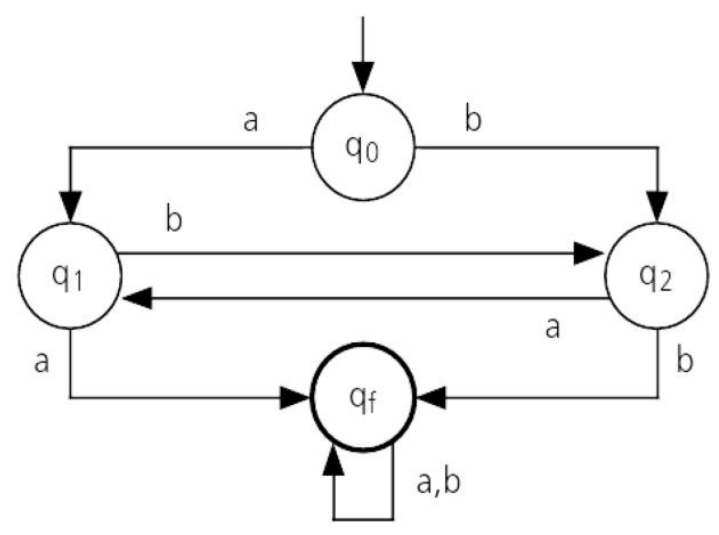
Para o autômato acima, podemos definir dois conjuntos:

1. Conjunto de estados Q:
2. Conjunto de alfabeto de entrada:

Todas as transição possíveis de um autômato finito são descritas por uma função parcial discreta , chamada de função de transição do autômato, onde (com base no diagrama acima):

O conjunto de todas as sequências possíveis de símbolos de é denotado por . Cada sequência é chamada de palavra (ou string) sobre o alfabeto . No caso do exemplo anterior, temos: Onde (epsilon) representa a palavra vazia, ou seja, a palavra que não possui símbolos.

É possível utilizar o conjunto para entender a função de transição para que seja possa operar sobre palavras, ou invés de cada símbolo do alfabeto . Em outras palavras, a função de transição estendida é tal que:

• se não lermos nenhum símbolo, então ficamos no mesmo estado
• , para e ao lermos uma palavra, a transição total sobre o autômato é uma composição das transições provocadas pela leitura de cada símbolo da palavra.

Para identificar a função de um autômato finito, é preciso considerar os seguintes elementos: 

• Conjunto de estados: Um conjunto finito e não vazio de estados
• Alfabeto: Um conjunto que define o alfabeto
• Função de transição: Uma função de transição
• Estado inicial: O estado inicial do autômato
• Conjunto de estados finais: Um subconjunto de estados que representa o conjunto de estados finais