Medidas de centro §

---

Média §

A média aritmética é a medida de centro mais simples para achar a média (mean) de um conjunto de observações e pode ser descrita a partir da seguinte fórmula:

Ou, em uma notação mais compacta:

A sua implementação em Python seria:

def arithmetic_average(x: List[int]):
  return sum(x) / len(x)

O símbolo (letra grega sigma maiúscula) tem o valor semântico de “some todas elas”. Além disso, é apenas uma maneira de diferenciar as observações. Por fim, (lê-se “x barra”) é uma representação amplamente utilizada para indicar a média. A média é sensível a influência de poucos outliers (valores atípicos). Em distribuições assimétricas, a média é puxada para a cauda longa. Pelo fato da média não poder resistir à influência de observações extremas, dizemos que não é uma medida resiste de centro.

Medida resistente é uma medida estatística que não é relativamente afetada por outliers na distribuição.

Exemplo 1 §

Suponha que temos o conjunto de dados: 5, 8, 12, 15, 20.

Portanto, a média desse conjunto é 12.

Exemplo 2 §

Suponha que temos o conjunto de dados: 5, 8, 12, 15, 20, 100.

Portanto, a média desse conjunto é 32.

Um ponto importante sobre as médias é que elas são sensíveis à influência de observações extremas (outliers), como foi possível notar após a inserção do valor 100 no conjunto do Exemplo 2. Desse modo, pelo fato da média não resistir à influência de outliers, logo dizemos que ela não é uma medida resistente de centro.

Medida resistente: é uma medida estatística que não é relativamente afetada por outliers (valores atípicos em pequena proporção no conjunto de dados).

Mediana §

A mediana (median) M é o ponto no meio da distribuição, ou seja, é o número tal que metade dos dados são menores do que ele, e metade, maior.

Primeiramente é necessário ordenar em ordem crescente os dados. Após isso, com base no número de elementos aplicamos a seguinte fórmula:

• Se o número de elementos for par, então:

  Considere a seguinte lista de valores para esse casos:

  Fazemos a média dos 2 elementos centrais da lista de valores.

• Se o número de elementos for ímpar, então:

  Considere a seguinte lista de valores para esse casos:

  Obtemos o elementos central da lista de valores.

Para descobrir a posição da mediana em um conjunto, basta utilizar a fórmula abaixo:

Sendo o número de elementos desse conjunto.

Exemplo 1 §

Suponha que temos seguinte o conjunto de dados: 5, 8, 10, 12, 15, 15, 20, 20, 25, 30, 35, 35, 40,40, 70.

Com base no conjunto de dados acima, sabemos que o número de elementos é 15, ou seja, e é ímpar, então temos:

Logo a mediana é o 8º elemento do conjunto, 20, ou seja, a mediana M tem valor de 20.

Exemplo 2 §

Agora suponha que temos o conjunto de dados:

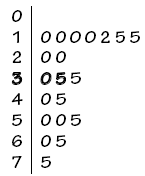
Nesse caso temos um número par de elementos, logo não há um elemento central, mas sim um par central sendo eles 30 e 35, pois há 9 elementos antes e depois desse par.

Agora vamos calcular a média aritmética desse par central para encontrarmos a mediana:

A seguir vamos obter a localização dessa mediana:

A localização representa que a mediana está “no meio do caminho” entre 10º e 11º elemento do conjunto, não indica um elemento exato do conjunto.

Comparação entre média e mediana §

Em distribuição simétrica, os valores da média e mediana são iguais. Se a distribuição é exatamente simétrica, os valores da média e da mediana são exatamente iguais. Já em uma distribuição assimétrica, a média, está mais próxima da cauda longa do que a mediana.

Muitas variáveis econômicas têm distribuições assimétricas à direita. Por exemplo, a doação mediana de faculdades e universidades nos EUA e Canadá, em 2018, foi de cerca de US 770 milhões. A maioria das instituições tem doações modestas, mas algumas poucas são muito ricas. A doação para Harvard foi de mais de US$ 38 bilhões. As poucas instituições ricas puxam a média para cima, mas não afetam a mediana. Relatórios sobre rendas e outras distribuições fortemente assimétricas em geral dão a mediana (“ponto médio”) em lugar da média (“média aritmética”).

Moda §

A moda de um conjunto de dados é o elemento com a maior frequência e é aplicado tanto para dados numéricos quanto categóricos, diferentemente da média e mediana suportando apenas dados numéricos.

Exemplo §

Suponha que você tenha uma lista de idades de um grupo de pessoas: 25, 30, 28, 25, 32, 25, 28, 29, 30, 28.

Para encontrar a moda nesse conjunto de dados, você identificaria o valor que mais se repete, ou seja, a idade que aparece com maior frequência. Nesse caso, a idade “25” aparece três vezes, mais do que qualquer outra idade. Portanto, a moda é 25.

Simetria de distribuições §

Uma distribuição é classificada como:

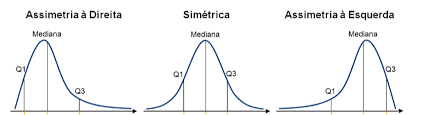
• Assimétrica à direita se a curva de frequência de uma distribuição tem uma “cauda” mais longa à direita da ordenada máxima (moda);

• Assimétrica à esquerda se a curva de frequência de uma distribuição tem uma “cauda” mais longa à esquerda da ordenada máxima (moda);

• Simétrica se os dados são distribuídos igualmente em torno da média.

Veja a figura abaixo que resume a simetria de uma distribuição:

Referências §

---