Medidas de variabilidade §

---

Quartis §

Os quartis são valores que dividem um amostra de dados em 4 partes iguais e é muito útil para entender a dispersão dos dados em um conjunto. O primeiro quartil corresponde a um valor superior a 25% dos dados da amostra. Já o segundo quartil é a mediana que corresponde ao valor divide pela metade o conjunto de dados. Por fim, o terceiro quartil é o valor que é superior a 75% dos dados amostrais.

Para realizar o cálculo dos quartis é necessário realizar as seguintes etapas:

1. Organizar os dados da lista em ordem crescente e então calcular a mediana.

2. O primeiro quartil é a mediana dos dados localizados no lado esquerdo da mediana central na lista ordenada.

3. O terceiro quartil é a mediana dos dados localizados no lado direito da mediana central na lista ordenada.

A seguir está uma implementação em Python do cálculo dos quartis, supondo que a amostra de dados é a seguinte:

data = [10, 10, 10, 10, 12, 15, 15, 20, 20, 30, 35, 35, 40, 45, 50, 50, 55, 60, 65, 75]

from typing import List, Tuple
 
def calculate_median(data: List[int]) -> float:
    n = len(data)
    middle_index = n // 2
 
    if n % 2 == 0:
        return (data[middle_index - 1] + data[middle_index]) / 2
      
    return data[middle_index]
 
def calculate_quartiles(data: List[int]) -> Tuple[float, float, float]:
    data.sort()
    n = len(data)
    middle_index = n // 2
 
    q1_data = data[:middle_index]
    q3_data = data[middle_index + (n % 2):]
 
    q1 = calculate_median(q1_data)
    q2 = calculate_median(data)
    q3 = calculate_median(q3_data)
 
    return q1, q2, q3
 
q1, q2, q3 = calculate_quartiles(data)
print(q1, q2, q3)

Saída:

(13.5, 32.5, 50.0)

A diferença entre o terceiro quartil (Q3) e o primeiro quartil (Q1) é conhecida como amplitude interquartil (AIQ) e é uma medida robusta de dispersão que minimiza a influência de valores extremos. A fórmula para o cálculo da AIQ é:

Onde:

• é o 3º quartil

• é o 1º quartil

Considerando o conjunto de dados utilizado anteriormente, a amplitude interquartil (AIQ) é:

A medida AIQ é especialmente útil para identificar outliers em uma amostra, pois pode ser considerado como atípico se esse registro apresentar um valor que ultrapasse em relação ao 1º quartil ou 3º quartil. Veja o exemplo abaixo:

Suponha um novo conjunto de dados com os seguintes valores:

data = [10, 10, 10, 10, 12, 15, 15, 20, 20, 30, 35, 35, 40, 45, 50, 50, 55, 60, 65, 75, 150]

def get_outliers(data: List[int]) -> List[int]:
  q1, q2, q3 = calculate_quartiles(data)
  aiq = q3 - q1
 
  return [
    x
    for x in data
    if x < q1 - 1.5 * aiq or x > q3 + 1.5 * aiq
  ]

O código acima é uma função que aplicar o critério descrito anteriormente para identificar os outliers de uma conjunto de dados. Em seguida vamos obter os valores atípicos da amostra data:

print(get_outliers(data))

Saída:

[150]

O resultado acima está correto, pois ao construir o gráfico de caixa (boxplot), que fornecem uma representação visual da dispersão dos dados e de possíveis assimetrias na distribuição, é possível observar a presença de um outliers na amostra com o valor de 150, como mostra a figura abaixo:

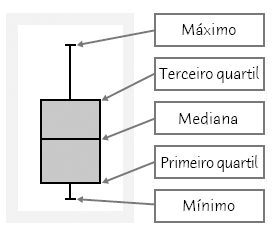
O resumo dos cinco números, que consiste na mediana, nos quartis e na menor e na maior observação. Ele fornece uma descrição geral rápida de uma distribuição. A mediana descreve o centro, e os quartis e os extremos mostram a dispersão. O gráfico boxplot se baseia no resumo dos cincos números.

Desvio padrão §

O desvio padrão é uma medida de variabilidade estatística que indica a dispersão dos valores em um conjunto de dados em relação à média. Ele é particularmente útil para avaliar o quão “espalhados” os valores estão ao redor da média. Em outras palavras, o desvio padrão fornece uma ideia da amplitude típica da distribuição dos valores.

O desvio padrão é calculado como a raiz quadrada da variância. A variância mede a média dos desvios ao quadrado dos valores em relação à média, enquanto o desvio padrão traz essa medida de volta para a mesma escala do conjunto de dados original, facilitando a interpretação.

A fórmula para calcular o desvio padrão populacional é:

Onde:

• é o número total de observações no conjunto de dados.

• é cada valor individual no conjunto de dados.

• é a média dos valores no conjunto de dados.

Para o desvio padrão amostral, a fórmula é ligeiramente ajustada para corrigir o viés:

Onde:

• é o número de observações no conjunto de dados amostral.

• é a média amostral dos valores.

O valor de deve ser sempre maior ou igual a zero; somente quando não há variabilidade, resumidamente, todos os valores do conjunto de dados devem ser iguais. Caso contrário, , então aumenta à medida que as observações se tornam mais dispersas em torno da média.

A “média” na variância divide a soma dos desvios por ou invés de , isso porque , ou seja, conhecendo observações, então determina-se o último a fim de manter essa igualdade. Pela fato de apenas dos desvios quadráticos poder variar livremente, a média dos desvios ao quadrado é dividido por . Dessa forma, o número é chamado de grau de liberdade da variância ou desvio padrão.

Vale lembrar que o desvio padrão e a variância não são medidas resistentes, ou seja, são sensíveis à influência de outliers.

O desvio padrão é uma medida importante porque expressa a dispersão dos valores em termos dos mesmos tipos de unidades que os dados originais, o que torna mais fácil comparar diferentes conjuntos de dados ou avaliar a variabilidade relativa entre eles. Um desvio padrão maior indica maior dispersão dos valores, enquanto um desvio padrão menor indica menor dispersão e que os valores estão mais próximos da média.

Referências §

---