Teste Z §

---

Teste Z (ou estatística Z) é um teste para hipótese sobre a média populacional , sob as condições simples de inferência, para introduzir os testes de significância.

Esse teste consiste em:

1. Dados amostrais que ocorreriam raramente se a hipótese nula fosse verdadeira fornecem evidência de que não é verdadeira;
2. O valor P nos dá uma probabilidade para medir “ocorreriam raramente”.

Exemplo §

Suponha uma AAS de tamanho de uma população Normal que tenha média desconhecida e desvio-padrão conhecido. Para testar a hipótese nula de que tenha um valor especificado,

Note

A afirmação da de que , pois a ideia central hipótese nula consiste em ser uma afirmativa de que não há qualquer efeito presente (^8be494), ou seja, a única forma de ter um resultado que não afete o teste Z é quando a média populacional for igual ao .

Calcule a estatística de teste Z de uma amostra da população:

Note

A estatística Z tem distribuição Normal padrão , pois a fórmula do teste Z é uma variação da Z-score que por sua vez serve para padronização dos dados, ou seja, torna a média e o desvio padrão .

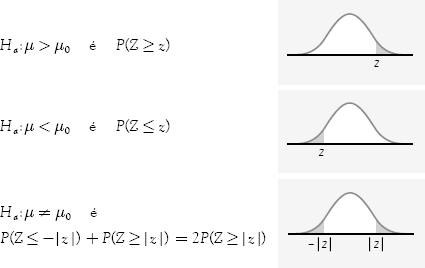
Considere uma variável Z com distribuição Normal padrão, o valor P para um teste de contra:

Referências §

---

A Estatística Básica e sua Prática