Função de ativação na camada oculta de redes multicamada
Para ilustrar um problema não linearmente separável, consideremos a tarefa de separar os valores 0 e 1 com base em uma tabela contendo os atributos previsores “x1” e “x2”, bem como o atributo meta “Classe”, que segue a lógica do operador lógico XOR (“ou exclusivo”).
| x1 | x2 | Classe |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
A nossa meta é identificar a correlação entre os atributos x1 e x2 para prever o valor do atributo meta “Classe”. Para essa tarefa, faremos uso de uma rede neural de múltiplas camadas Perceptron com uma camada oculta contendo 3 neurônios, cada um com seus respectivos pesos:
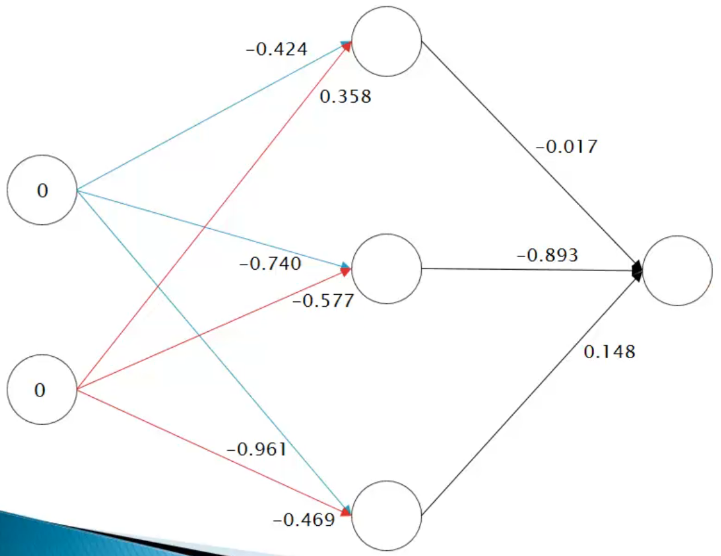
O primeiro passo é calcular a soma ponderada para cada neurônio na camada oculta, utilizando a seguinte fórmula:
A seguir, o resultado da soma é inserido na função sigmoide como parâmetro “x” e aplicado para cada neurônio, conforme a equação:
Depois de obtermos os resultados para cada neurônio, repetimos o processo de soma ponderada e ativação, desta vez utilizando os valores obtidos na função sigmoide. Isso nos leva ao resultado final para o primeiro registro da tabela.
É crucial repetir todo esse processo para cada entrada da tabela, ajustando os pesos ao longo do caminho a fim de minimizar os erros e permitir que a rede neural aprenda a relação não linear entre os atributos de entrada e a saída desejada.