Sistema de numeração
Objetivos
-
Revisar os sistemas de numeração decimal, binário, hexadecimal e octal;
-
Conhecer a representação interna e conversões típicas em sistemas computacionais;
-
Praticar com representação de dados numéricos nos diversos sistemas de numeração.
Sistema de numeração posicional
A arquitetura de von Neumann é uma arquitetura que propôs que as instruções para o seu funcionamento fossem gravadas eletronicamente na memória do computador.
Dessa forma, os dados precisam de uma representação para armazená-las na memória do computador.
A representação convencional de dados é o sistema de numeração binária.
Em um sistema de numeração posicional, um dado numérico numa determinado base numérica representado por:
Pode ser representado por:
Existem 4 sistema de numeração posicional fundamentais na computação:
| Sistema | Base | Símbolos | Exemplos |
|---|---|---|---|
| Binário | 2 | 0, 1 | |
| Octal | 8 | 0, 1, 2, 3, 4, 5, 6, 7 | |
| Decimal | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | |
| Hexadecimal | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Para uma determinada base b, o maior dado numérico com k dígitos que pode ser representado nesta base é dado por:
Exemplo
Para representar uma quantidade de “dois mil, trezentos e sessenta e quatro” elementos, usa-se a seguinte notação:
-
Sistema binário: (12 dígitos)
-
Sistema octal: (4 dígitos)
-
Sistema decimal: (4 dígitos)
-
Sistema hexadecimais: (3 dígitos)
Como é possível observar, a vantagem de se utilizar um sistema de numeração com mais símbolos (com base maior) é que o número requer menos dígitos para ser armazenado.
Conversão de qualquer base para decimal
Para converter um número de qualquer base para decimal, basta utilizar a seguinte fórmula:
Onde:
-
é o número a ser convertido para base decimal
-
é a posição do último algarismo do número
-
é a posição do primeiro algarismo do número
-
é o algarismo em um dada posição do número
-
é a base do número
Por exemplo, vamos converter o número para decimal:

Conversão de decimal para qualquer base
Parte integral (ou inteira):
Para converter um número decimal inteiro para qualquer base, basta realizar divisões sucessivas pela base do número original até o quociente der , após isso basta copiar o resto das divisões de baixo para cima.
Veja um exemplo da conversão do número para a base 2:
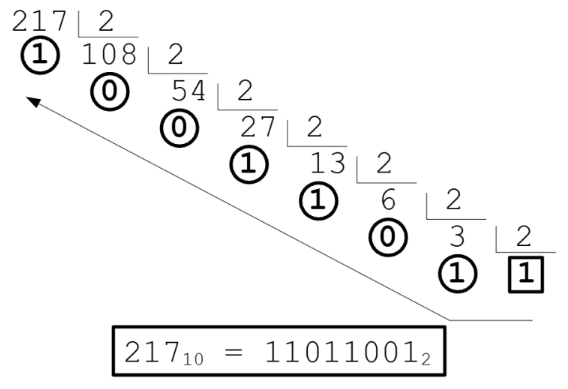
Parte fracionária:
Para converter uma fração decimal para qualquer base, você deve realizar multiplicações sucessivas pela base do número original até que não haja mais dígitos significantes (!= de 0) ou quando a precisão desejada for alcançada, e no final basta copiar o valor inteiros do produto de cima para baixo.
Abaixo estão alguns exemplos desse tipo de conversão:

Parte fracionário com dízima periódica:
Para converter uma fração decimal com dízima periódica para qualquer base, basta seguir o processo descrito acima, porém no final do número convertido adicione "" (reticências) para indicar é uma dízima.

Sistema binário
No sistema binário, o dígito pode ser representado pelos símbolos 0 e 1.
Os equipamentos eletrônicos precisos utilizam apenas 2 níveis de tensão.
A menor unidade no sistema binário é chamado de bit (ou binary digit).
Além disso, é importante entender os termos MSB e LSB:
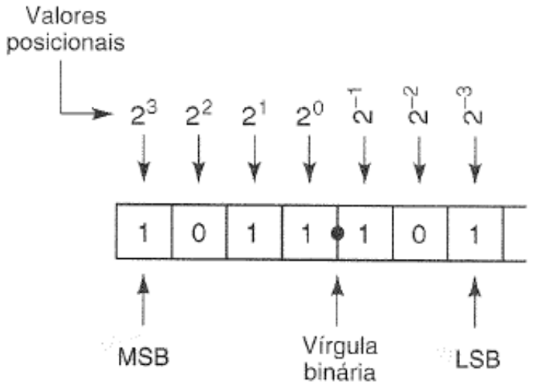
-
Most Significant Bit (MSB) é o dígito com o maior valor posicional
-
Least Significant Bit (LSB) é o dígito com o menor valor posicional
Sequência de contagem binária
A tabela a seguir mostra a conversão entre número binários e seus respectivos valores em decimal:
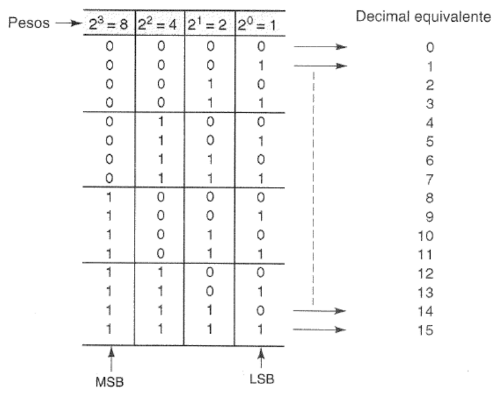
A maioria dos microcomputadores manipulam e armazenam dados binários em grupos de 8 bits, também chamado de byte (sendo a unidade básica em computação)
O maior valor que um byte pode armazenar é .
Uma unidade inferior também é definida como nibble ou nyble como um conjunto de 4 bits.
Conversão de octal-binário
Para a conversão de octal-binário, cada dígito octal equivale a 3 dígitos binários.

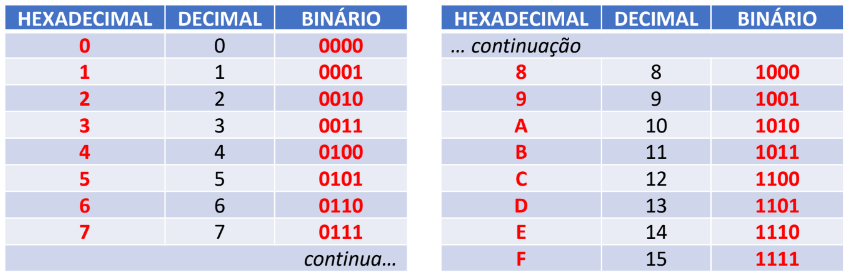
Conversão hexadecimal-binário
Para a conversão de hexadecimal-binário, cada dígito hexadecimal equivale a 4 dígitos binários.
Unidades de medida
O computar utiliza o sistema numérico binário para representar quantidades, diferentemente dos seres humanos que adotam o sistema decimal.
Para a representação de 1 caractere (letra, número, símbolo gráfico, etc) é necessário 8 bits ou 1 byte, ou seja, para armazenar a palavra DIGITAL na memória é necessário de 7 bytes para tal.
Múltiplos (SI)
Pelo byte ser a unidade fundamental da computação para armazenamento de dados em um computador, exitem os seus múltiplos de acordo com o Sistema Internacional de Unidades (SI):

Múltiplos (IEC)
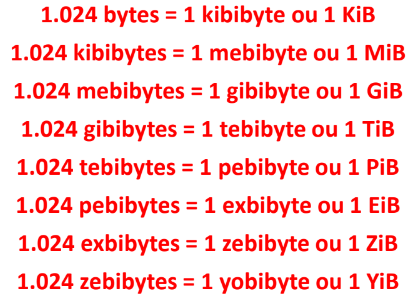
Como o computador utilizam o sistema de numeração binária, os prefixos do Sistema Internacional (SI) de Unidades não permitem indicar a capacidade correta de armazenamento, uma vez que são baseados no sistema decimal. Dessa forma, a Comissão de Eletrotécnica Internacional (IEC) estabeleceu os seguintes múltiplos:
Endianness
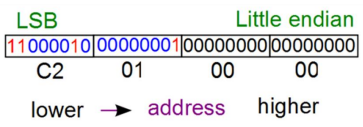
Endianness é uma característica na arquitetura de computadores que se refere à ordem na qual os bytes de um valor multibyte (como um número inteiro de 32 bits) são armazenados na memória. Em outras palavras, é a forma como os bytes individuais que compõem um dado multibyte são organizados na memória.
Existem dois tipos principais de endianness:
-
Big-endian:o byte mais significativo (MSB) é armazenado no endereço de memória mais baixo, ou seja, no primeiro byte de memória. Os bytes subsequentes são armazenados em ordem decrescente de significância.
-
Little-endian: o byte menos significativo (LSB) é armazenado no endereço de memória mais baixo, ou seja, no primeiro byte de memória. Os bytes subsequentes são armazenados em ordem crescente de significância.
A escolha entre big-endian e little-endian afeta diretamente como os dados são lidos e interpretados pelo hardware, e isso é particularmente importante ao se lidar com sistemas que têm diferentes endianness.
Por exemplo, imagine o número inteiro de 32 bits “0x000001C2”. Em uma arquitetura big-endian, ele seria armazenado na memória da seguinte forma:

Enquanto que em uma arquitetura little-endian, ele seria armazenado dessa forma:
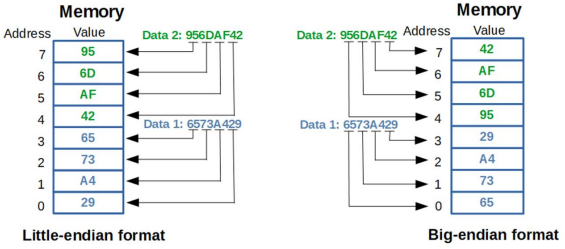
Abaixo está um exemplo de como 2 dados inteiros de 32 bits são armazenados em memória usando as arquiteturas little-endian e big-endian:
Representação de quantidades binárias em aplicações
Um dispositivo eletrônico processa uma informação na forma binária com dois possíveis estados, 0 e 1.
A seguir dois exemplos sobre a representação desses sistemas:
No exemplo “a” o cartão não furado representa o nível binário 0, já o furado indica o nível binário 1. O exemplo “b” segue a mesma lógica, a válvula aberta representa o nível binário 0, já a fechada indica o nível binário 1.
Representação de quantidades binárias em circuitos eletrônicos
A representação binária em circuitos digitais (CIs) é feito por meio dos níveis de tensão em Volts:
Codificação
A codificação é a representação de números, letras ou palavras por meio de um combinação de símbolos. O código é o grupo de símbolos.
Por exemplo, o código Morse é a representação de letras do alfabeto por meio de um combinação específica de traços e pontos.
A representação de um número decimal em binário é denominado de codificação binária pura.
Código decimal codificado em binário (BCD)
O Código Decimal Codificado em Binário (BCD) é uma forma de representar números decimais usando uma codificação binária. Ele é frequentemente usado em aplicações que envolvem saída para displays digitais, como voltímetros digitais, contadores de frequência, calculadoras e outros dispositivos que exibem valores numéricos.
Em um número decimal, cada dígito (0 a 9) é representado por quatro bits em BCD para garantir que todos os dígitos possam ser representados. Portanto, cada número decimal de 0 a 9 é codificado usando 4 bits.
A seguir está um tabela de conversão dos principais sistema de numeração em BCD:
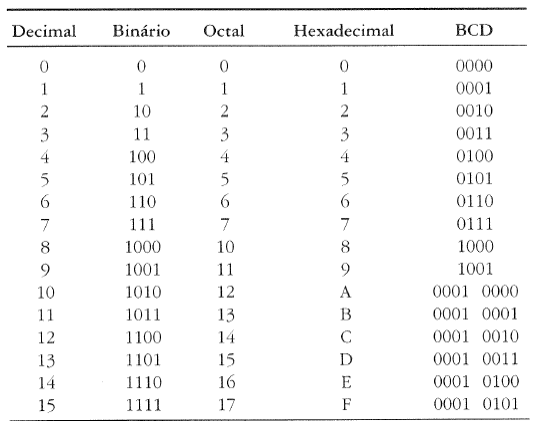
O BCD é usado especialmente quando é necessário exibir números em displays digitais, porque cada dígito pode ser diretamente convertido em sua representação BCD e, em seguida, exibido no display.
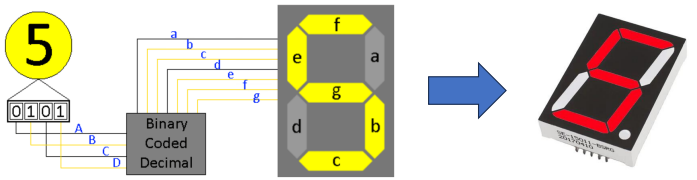
Essa codificação é mais intuitiva para humanos, uma vez que está diretamente relacionada aos dígitos decimais que usamos no dia a dia. No entanto, ela não é tão eficiente em termos de utilização de bits como outras codificações como a binária pura, a hexadecimal ou a octal.
Código ASCII
ASCII (American Standard Code for Information Interchange) é um conjunto de códigos de caracteres amplamente utilizado para representar caracteres alfanuméricos e símbolos em computadores. Ele é uma das primeiras codificações de caracteres padronizadas e tem sido fundamental para a comunicação de texto em sistemas de computador.
O ASCII é um código de 7 bits, o que significa que ele utiliza 7 bits para representar cada caractere. Isso permite 128 combinações diferentes, o que é suficiente para representar os caracteres do alfabeto, números, sinais de pontuação e alguns caracteres especiais.
A unidade básica de armazenamento em computadores modernos é o byte (8 bits), e com isso o cada símbolo ASCII pode ser armazenado em um byte, com o bit mais significativo sendo sempre zero. Isso significa que um caractere ASCII é representado pelos 7 bits do ASCII original, com um bit zero adicionado à esquerda que indica a integridade de um sequência de caracteres transmitidos em rede de computadores, por exemplo.
A seguir a tabela com a representação binária de cada símbolo ASCII:
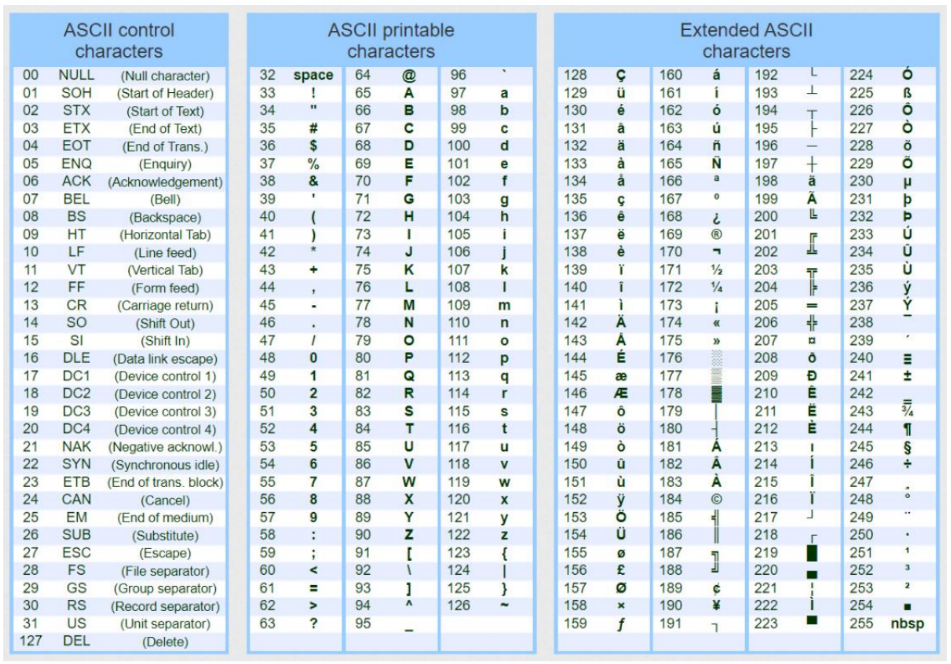
Código ISO-8859-1
O código ISO-8859-1, também conhecido como Latin-1, é uma codificação de caracteres que estende o conjunto ASCII para incluir caracteres acentuados e outros símbolos utilizados em diversos idiomas europeus, incluindo o português. O ISO-8859-1 é uma evolução do ASCII, projetado para acomodar línguas que contêm caracteres especiais, como acentos, cedilhas e outros símbolos gráficos.
Enquanto o ASCII original utiliza apenas 7 bits para representar caracteres, o ISO-8859-1 utiliza 8 bits (1 byte), o que permite a inclusão de um conjunto mais amplo de caracteres. O ISO-8859-1 é uma codificação amplamente utilizada em países de língua latina, como o Brasil, para representar caracteres com acentuação, como á, é, í, ó, ú, ç, entre outros.
O conjunto de caracteres do ISO-8859-1 inclui 191 símbolos imprimíveis, como letras maiúsculas e minúsculas, números, símbolos de pontuação e caracteres acentuados e não tem como objetivo
No entanto, o ISO-8859-1 tem suas limitações, pois não abrange todos os caracteres necessários para idiomas de todo o mundo. Por exemplo, idiomas que utilizam caracteres não latinos, como os caracteres chineses, japoneses, árabes e cirílicos, não são abrangidos por essa codificação. Devido a essas limitações, surgiu a necessidade de codificações mais abrangentes, como o Unicode, que permite a representação de uma ampla gama de caracteres de diferentes idiomas e culturas em uma única codificação.
Codificação Unicode
O Unicode é um padrão universal de codificação de caracteres que tem como objetivo mapear todos os tipos de símbolos utilizados em sistemas de escrita de diferentes idiomas ao redor do mundo. Ele vai além dos símbolos de escrita e inclui também símbolos matemáticos, formas geométricas e outros tipos de caracteres. O Unicode é uma solução para o desafio de representar uma ampla gama de caracteres em diferentes idiomas e sistemas de escrita de maneira consistente e unificada.
O padrão Unicode abrange mais de 107 mil símbolos mapeados, que são gerenciados pelo Unicode Consortium, uma organização sem fins lucrativos que coordena o desenvolvimento e a promoção do Unicode.
O Unicode é implementado através de várias codificações conhecidas como UTF (Unicode Transformation Format). Essas codificações definem como os caracteres Unicode são representados em bytes, permitindo a transferência e armazenamento eficientes de texto em diferentes sistemas e dispositivos.
Existem várias variações do UTF, incluindo:
-
UTF-8 (UCS): É uma codificação de comprimento variável que utiliza 8 bits para representar caracteres ASCII, mas pode usar até 32 bits para caracteres não ASCII. Ela é eficiente para textos predominantemente em inglês e outras línguas ocidentais, pois utiliza menos espaço para esses caracteres e expande conforme necessário para caracteres não ASCII.
-
UTF-16 (UCS-2): Utiliza 16 bits para representar a maioria dos caracteres comuns. É adequado para muitos idiomas e scripts.
-
UTF-32 (UCS-4): Usa sempre 32 bits para representar cada caractere. Isso garante que todos os caracteres Unicode sejam representados de maneira uniforme, mas pode consumir mais espaço em comparação com outras codificações.
O Unicode resolveu muitos dos problemas de incompatibilidade de codificação que surgiram quando os sistemas computacionais precisavam lidar com uma diversidade crescente de idiomas e sistemas de escrita. Ele permitiu a comunicação e troca de dados entre diferentes culturas e idiomas, bem como a representação consistente e precisa de texto em plataformas e dispositivos diversos.