Merge Sort §

---

A operação de merge sort é um algoritmo de ordenação que segue a abordagem dividir e conquistar. Ele divide a lista não ordenada em sub-listas, cada uma contendo um único elemento, e então mescla essas sub-listas repetidamente para produzir novas sub-listas ordenadas até que reste apenas uma sub-lista, que é a lista ordenada final.

Note

O merge sort garante uma complexidade de tempo de onde é o número de elementos na lista.

Passo a passo do algoritmo merge sort:

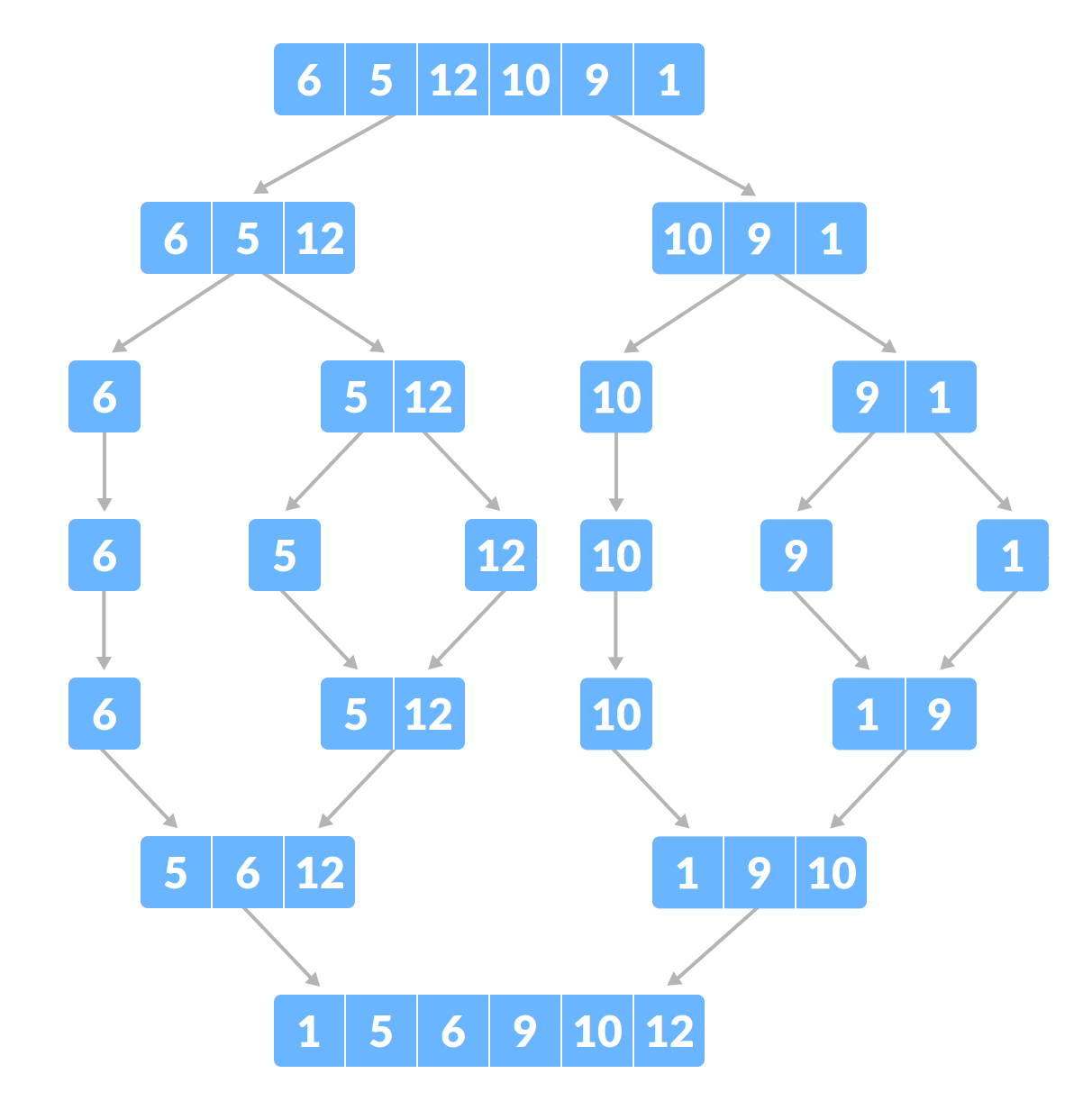
1. Divisão: Divida a lista não ordenada em duas sub-listas de tamanho aproximadamente igual até que a sub-lista tenha tamanho igual ou inferior a 1.
2. Conquista: Mescla as sub-listas ordenadas para produzir uma nova lista ordenada. Isso é feito comparando os elementos das sub-listas e mesclando-os em ordem crescente.

Implementação em C:

#include <stdio.h>
#include <stdlib.h>
 
void merge(int arr[], int l, int m, int r) {
    int i, j, k;
    int n1 = m - l + 1;
    int n2 = r - m;
 
    // Cria sub-arrays temporários
    int L[n1], R[n2];
 
    // Copia os dados para os sub-arrays L[] e R[]
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];
 
    // Mescla os sub-arrays de volta para o array original arr[l..r]
    i = 0; // Índice inicial do primeiro sub-array
    j = 0; // Índice inicial do segundo sub-array
    k = l; // Índice inicial do array mesclado
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
 
    // Copia os elementos restantes de L[], se houver algum
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
 
    // Copia os elementos restantes de R[], se houver algum
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}
 
void mergeSort(int arr[], int l, int r) {
    if (l < r) {
        // Encontra o ponto médio do array
        int m = l + (r - l) / 2;
 
        // Ordena a primeira metade e a segunda metade
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);
 
        // Mescla as partes ordenadas
        merge(arr, l, m, r);
    }
}
 
int main() {
    int arr[] = {12, 11, 13, 5, 6, 7};
    int arr_size = sizeof(arr) / sizeof(arr[0]);
 
    printf("Array original: \n");
    for (int i = 0; i < arr_size; i++)
        printf("%d ", arr[i]);
    printf("\n");
 
    // Chama a função mergeSort para ordenar o array
    mergeSort(arr, 0, arr_size - 1);
 
    printf("Array ordenado: \n");
    for (int i = 0; i < arr_size; i++)
        printf("%d ", arr[i]);
    printf("\n");
 
    return 0;
}

Referências §

---

APII-Semana14-MétodosDeOrdenação2