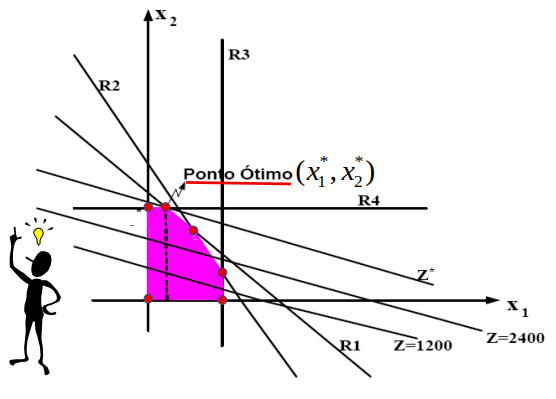
Técnica Geométrica
A Programação Linear é uma técnica para resolver problemas de otimização nos quais todas as relações entre as variáveis podem ser expressas linearmente.
A seguir o passo a passo para encontrar a solução geométrica para Problemas de Programação Linear em duas variáveis.
1. Formulação do problema
O problema geral de Programação Linear em duas variáveis (
Sujeita
Além disso, as variáveis devem ser não-negativas (restrição de não negatividade), ou seja,
2. Identificação das restrições
Cada restrição define uma reta ou semiplano no plano
As restrições podem ser do tipo
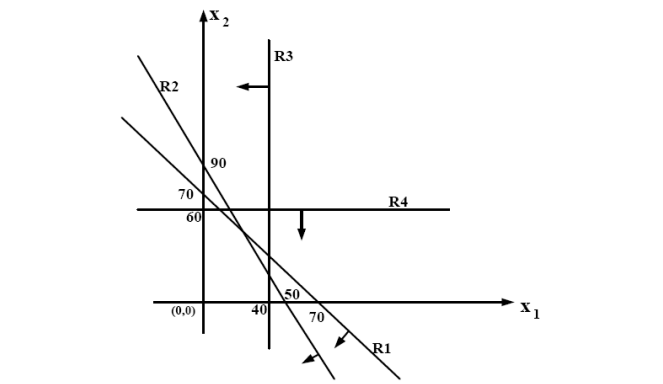
3. Região viável
A interseção de todos os semiplanos definidos pelas restrições forma a região viável.
É importante observar que a região viável é sempre uma interseção de um número finito de retas e planos.
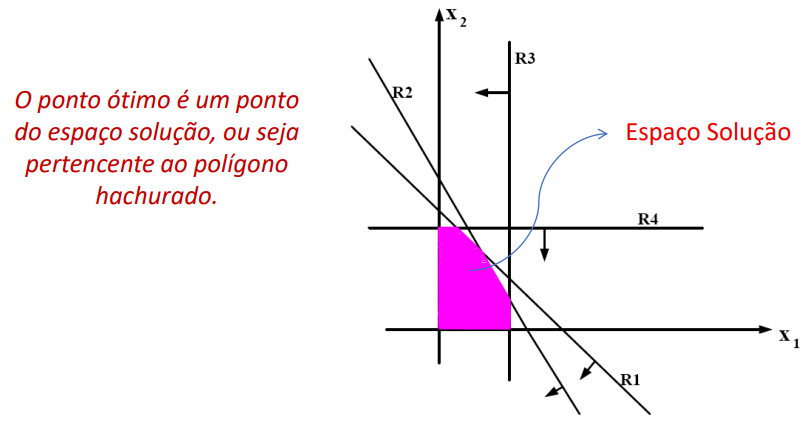
4. Pontos extremos da região viável
Os pontos onde duas ou mais restrições se encontram são chamados de pontos extremos.
Esses pontos são cruciais porque, de acordo com o Teorema dos Valores Máximos e Mínimos , a solução ótima ocorre em um desses pontos, se a região viável for limitada.
5. Solução ótima
O objetivo é encontrar uma solução viável que maximize ou minimize a função objetivo.
Uma vez que a região viável e os pontos extremos são identificados, determinamos qual deles otimiza a função objetivo.
6. Aplicação do Teorema dos Valores Máximos e Mínimos
-
Se a região viável é limitada e não vazia, a função objetivo atinge tanto um valor máximo quanto um valor mínimo, e esses valores ocorrem nos pontos extremos.
-
Se a região viável é ilimitada, pode ou não haver um máximo ou mínimo. No entanto, se existir, ocorrerá em um ponto extremo.
7. Resolução e Verificação
Finalmente, aplicamos o Teorema dos Valores Máximos e Mínimos para resolver o problema e verificar a solução encontrada.
