PCA

A classe PCA (Principal Component Analysis) no módulo sklearn.decomposition do Scikit-Learn é uma implementação da técnica de análise de componentes principais. A PCA é uma técnica de redução de dimensionalidade que é amplamente usada na análise de dados e aprendizado de máquina para simplificar conjuntos de dados complexos, preservando as informações mais importantes e reduzindo a dimensionalidade dos dados.

Sintaxe §

from sklearn.decomposition import PCA
 
pca = PCA()

Principais atributos §

• explained_variance_: Este atributo contém a quantidade de variação explicada por cada componente principal.

• explained_variance_ratio_: Este atributo contém a proporção da variação total explicada por cada componente principal.

• components_: Este atributo contém os vetores dos componentes principais, que são as direções ao longo das quais os dados têm a maior variação.

• n_components: Especifica o número de componentes principais a serem mantidos após a redução de dimensionalidade. Se for definido como None, todos os componentes principais serão retidos. Você pode definir um número inteiro específico para reduzir a dimensionalidade para esse número de componentes.

Principais métodos §

• fit(X): Esse método é usado para ajustar o modelo PCA aos dados de entrada X. Ele calcula os componentes principais com base nos dados fornecidos.

• transform(X): Após ajustar o modelo com fit, você pode usar este método para transformar os dados de entrada X nos componentes principais.

• fit_transform(X): Este método combina os passos de ajustar o modelo com fit e transformar os dados com transform em um único passo.

• inverse_transform(X): Este método permite retornar os dados transformados para o espaço original.

Exemplo §

from sklearn.decomposition import PCA
import plotly.express as px
 
# Carregando os dados do cartão de crédito (substitua isso pelo seu conjunto de dados real)
base_credit_card = ...
 
# Selecionando as características relevantes do conjunto de dados
X_credit_card = base_credit_card.iloc[:, [1, 2, 3, 4, 5, 25]].values
 
# Padronizando os dados
scaler_credit_card = StandardScaler()
X_credit_card = scaler_credit_card.fit_transform(X_credit_card)
 
# Aplicando o algoritmo K-Means com 4 clusters
kmeans_credit_card = KMeans(n_clusters=4, random_state=0)
labels = kmeans_credit_card.fit_predict(X_credit_card)
 
# Aplicando PCA para reduzir a dimensionalidade de 6 para 2 componentes principais
pca = PCA(n_components=2)
X_credit_card_pca = pca.fit_transform(X_credit_card)
 
# Criando um gráfico de dispersão para visualizar os clusters após a redução de dimensionalidade
px.scatter(x=X_credit_card_pca[:, 0], y=X_credit_card_pca[:, 1], color=labels)

Saída:

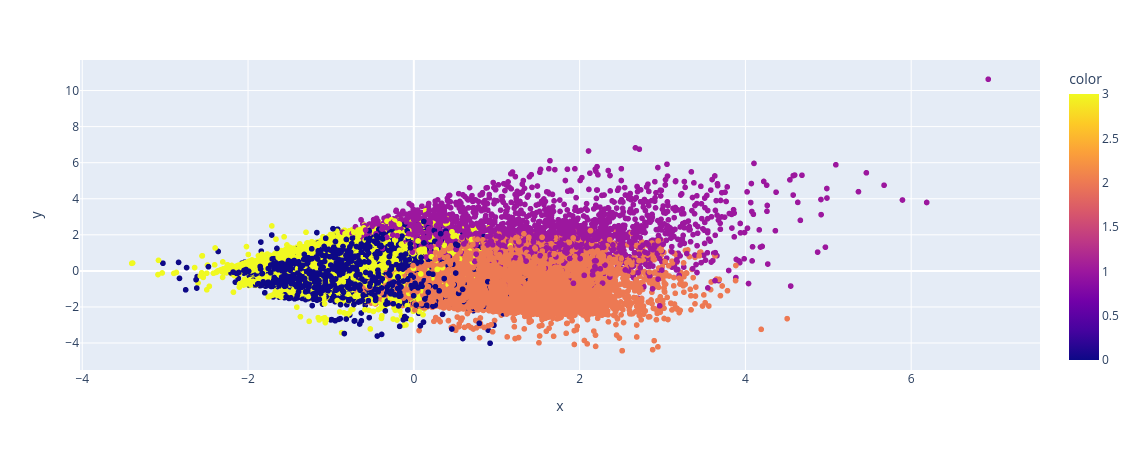
Neste exemplo, usamos o PCA para reduzir a dimensionalidade dos dados para 2 componentes principais, o que nos permite visualizar a distribuição dos clientes em clusters com mais facilidade. A coloração no gráfico representa os clusters identificados pelo algoritmo K-Means. Essa técnica pode ser útil para entender melhor como os clientes estão agrupados com base nas características selecionadas do cartão de crédito. Lembre-se de substituir base_credit_card pelos seus próprios dados ao aplicar esse exemplo ao seu problema específico.

A PCA é frequentemente usada para pré-processamento de dados, visualização de dados, redução de dimensionalidade e, às vezes, para eliminar a multicolinearidade em conjuntos de dados. Ao reduzir a dimensionalidade dos dados, a PCA pode ser uma ferramenta útil para acelerar algoritmos de aprendizado de máquina e melhorar o desempenho do modelo. Também é uma técnica útil para explorar a estrutura subjacente dos dados e para visualizar dados em um espaço de menor dimensionalidade.