A classe KMeans do módulo sklearn.cluster é uma implementação do algoritmo K-Means, que é uma técnica de aprendizado não supervisionado para análise de agrupamento. O K-Means é amplamente utilizado para particionar um conjunto de dados em grupos (clusters) com base na similaridade entre os pontos de dados.
Sintaxe
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, init='k-means++', max_iter=300, n_init=10, random_state=0)Principais parâmetros
-
n_clusters: Especifica o número de clusters a serem formados. Este é um parâmetro importante que você precisa definir com base no conhecimento do problema ou usando técnicas de seleção de número de clusters, como o método do cotovelo. -
init: Define a estratégia de inicialização dos centroides dos clusters. Pode ser ‘k-means++’ (inicialização inteligente para acelerar a convergência) ou ‘random’ (inicialização aleatória). -
max_iter: Define o número máximo de iterações para a convergência do algoritmo K-Means em um único run. -
n_init: Define o número de vezes que o algoritmo será executado com diferentes centroides iniciais. O resultado final será o melhor resultado entre várias execuções. -
random_state: Controla a semente para a geração de números aleatórios, garantindo que os resultados sejam reproduzíveis.
Principais atributos:
-
labels_: Este atributo contém uma matriz de rótulos que especifica a que cluster cada ponto de dados pertence. Cada rótulo é um número inteiro que representa o cluster. -
cluster_centers_: Este atributo contém as coordenadas dos centroides finais de cada cluster após a convergência do algoritmo. É útil para entender onde estão localizados os clusters no espaço de atributos.
Principais métodos
-
fit(X): Este método é usado para treinar o modelo K-Means nos dados de entradaX. Durante o treinamento, o algoritmo encontra os centroides dos clusters e atribui rótulos aos pontos de dados. -
predict(X): Este método é usado para prever a qual cluster pertence cada ponto de dados emX, com base nos centroides previamente calculados durante o treinamento. -
fit_predict(X): Este método combina o treinamento e a previsão em uma única etapa. Ele ajusta o modelo aos dados de entradaXe retorna os rótulos de cluster para cada ponto de dados.
Exemplo
import plotly.express as px
import plotly.graph_objects as go
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
# Dados de exemplo - idade e salário
x = [20, 27, 21, 37, 46, 53, 55, 47, 52, 32, 39, 41, 39, 48, 48]
y = [1000, 1200, 2900, 1850, 900, 950, 2000, 2100, 3000, 5900, 4100, 5100, 7000, 5000, 6500]
# Organização dos dados em uma matriz numpy
base_salary = np.array([[age, salary] for age, salary in zip(x, y)])
# Padronização dos dados usando StandardScaler
scaler_salary = StandardScaler()
base_salary = scaler_salary.fit_transform(base_salary)
# Criação do modelo K-Means com 3 clusters
kmeans_salary = KMeans(n_clusters=3)
kmeans_salary.fit(base_salary)
# Obtenção dos centroides dos clusters e rótulos
centroides = kmeans_salary.cluster_centers_
labels = kmeans_salary.labels_
# Criação do gráfico de dispersão com cores representando os clusters
graph1 = px.scatter(x=base_salary[:, 0], y=base_salary[:, 1], color=labels)
# Criação do gráfico com os centroides destacados
graph2 = px.scatter(x=centroides[:, 0], y=centroides[:, 1], size=[12, 12, 12])
# Combinando os gráficos
graph3 = go.Figure(data=graph1.data + graph2.data)
# Exibição do gráfico resultante
graph3.show()Saída:
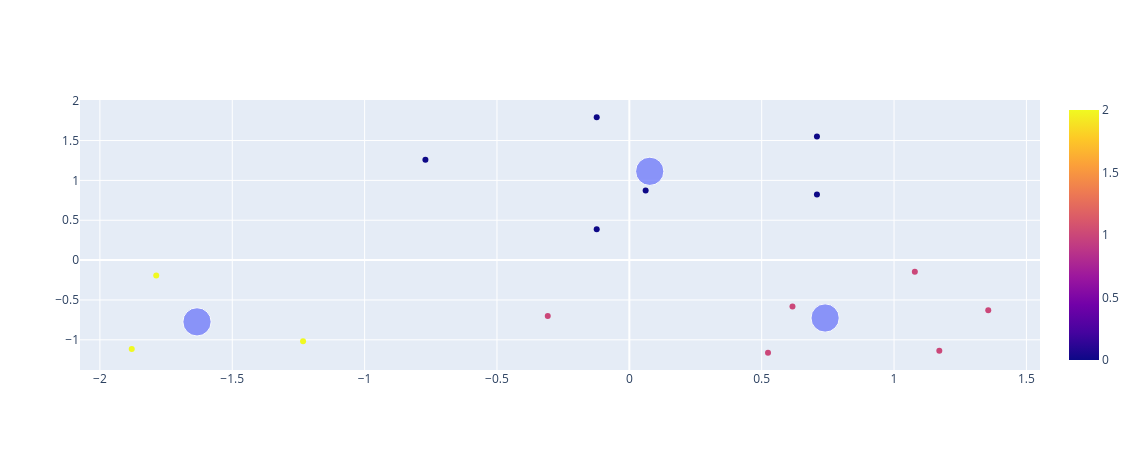
Neste exemplo, os dados de idade e salário foram padronizados e agrupados em três clusters distintos usando o algoritmo K-Means. O gráfico de dispersão mostra os pontos de dados coloridos de acordo com os clusters atribuídos, e os centroides dos clusters são representados por círculos maiores.
O K-Means é uma técnica eficaz para agrupar dados em clusters, mas é importante escolher cuidadosamente o número de clusters e pré-processar os dados, se necessário, antes de aplicar o algoritmo. Além disso, a interpretação dos resultados dos clusters também é uma parte crítica da análise de agrupamento.