Árvore AVL §

---

Note

A árvore AVL foi fruto de uma pesquisa de dois matemáticos soviéticos (Georgii Maximovich Adelson-Velskii e Evgenii Mikhailovich Landis) publicado no artigo de 1962.

Uma árvore binária é dita como AVL quando, para qualquer nó de , a diferença entre a altura das subárvores esquerda e direita é no máximo igual a 1 em módulo.

Note

Alguns autores chamam a árvore AVL de height-balanced tree, ou árvore com altura balanceada.

Uma BSTpode ser considerada uma AVL quando é no máximo igual a 1. Devido a essa relação entre AVL, BST e consequentemente com aÁrvore binária, podemos representá-la a partir a hierarquia abaixo:

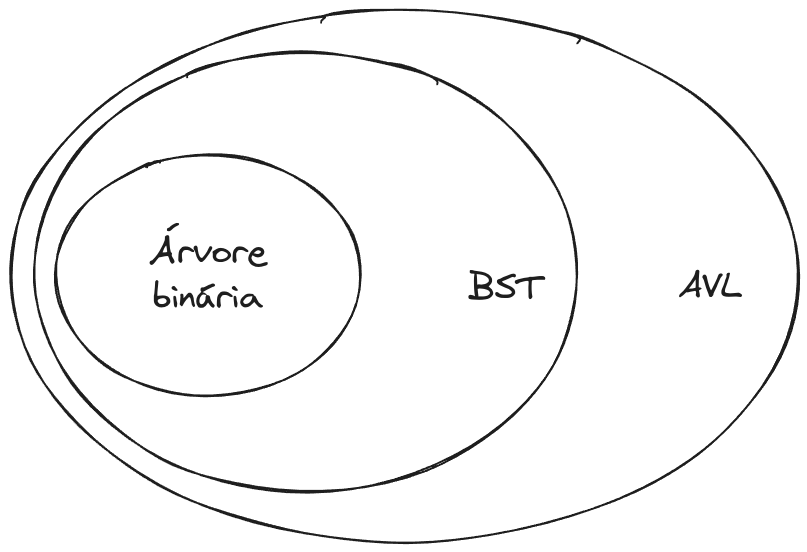
Árvores balanceadas, como a AVL, são uma solução performática para operações de buscas (em ), diferentemente das árvores desbalanceadas (como a árvore binária e BST) que performam em tempo , pois essa operação está diretamente ligada a altura da árvore.

Note

As operações de busca, inserção e remoção possuem complexidade .

Exemplos de árvores balanceadas

, , AVL, Rubro-Negras

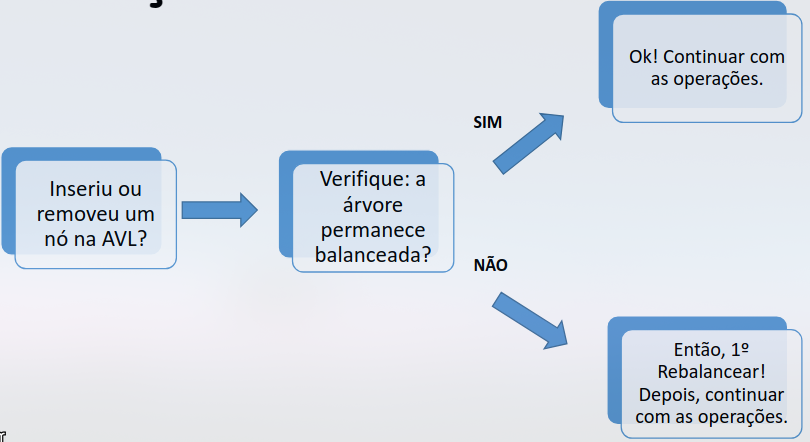
Vale ressaltar que a operação de inserção e deleção dos elementos de um árvore é feito de forma recursiva, dessa forma, o balanceamento é feito na volta de cada chamada na pilha de recursão, verificando se a subárvore atual está balanceada ou não com base no fator de balanceamento.

Note

Pelo fato do balanceamento ser feito na volta de cada chamada recursiva, apenas os nós percorridos para realizar a alteração da árvore (seja uma inserção ou remoção) serão balanceados, caso for necessário. Com isso otimizando o algoritmo de balanceamento.

Referências §

---

Aula 3 - Árvore AVL

Aula 10 de laboratório - Árvore AVL