Distribuição T
Testes e intervalos de confiança para a média µ de uma população Normal se baseiam na média amostral x de uma AAS. Pelo Teorema do Limite Central, os procedimentos resultantes são aproximadamente corretos para outras distribuições populacionais, quando a amostra é grande.
Observação
A média amostral padronizada é a estatística Z de uma amostra,
Se o desvio padrão
é conhecido, então usaríamos a estatística Z e a distribuição Normal padrão.
Na distribuição T, o desvio padrão
A figura abaixo compara as curvas de densidade da distribuição Normal padrão com as distribuições 
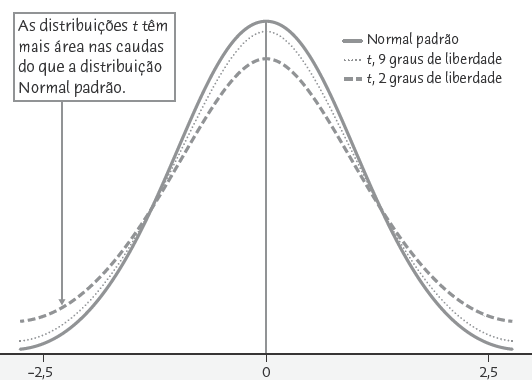
- As distribuições
são simétricas, têm um único pico e formato de sino, semelhantes à distribuição Normal padrão. - A dispersão das distribuições
é um pouco maior do que a da distribuição Normal padrão, com mais probabilidade nas caudas e menos no centro, refletindo a introdução de mais variação devido à estimativa em vez do parâmetro fixo .
À medida que os graus de liberdade aumentam, a curva de densidade da distribuição
O intervalo de confiança e o Teste T são precisos quando a distribuição da população é exatamente normal, embora dados reais nunca sejam exatamente normais. Na prática, a distribuição normal serve como uma excelente aproximação para a verdadeira distribuição dos dados em estudos reais. A eficácia dos procedimentos t depende da extensão em que são afetados pela falta de normalidade nos dados.
Procedimentos robustos, no contexto de intervalos de confiança ou testes de significância, são aqueles em que o nível de confiança ou valor P não sofre alterações significativas mesmo quando as condições para o uso do procedimento são violadas.