O boxplot, também conhecido como gráfico de caixa, é uma ferramenta poderosa para visualizar a distribuição de um conjunto de dados e identificar a presença de outliers. Ele fornece uma representação gráfica dos principais pontos estatísticos de um conjunto de dados e é especialmente útil para comparar várias distribuições lado a lado.
Construção de um boxplot:
Para criar um boxplot, siga estas etapas:
-
Ordenar os dados: Primeiro, ordene os dados em ordem crescente.
-
Calcular os Quartis: Em seguida, calcule três quartis:
- Primeiro Quartil (Q1): O valor que divide os 25% mais baixos dos dados.
- Segundo Quartil (Q2): O valor que divide os 50% do meio dos dados; é igual à mediana.
- Terceiro Quartil (Q3): O valor que divide os 25% mais altos dos dados.
-
Calcular os Limites dos Bigodes (Whiskers): Os bigodes são as linhas que se estendem a partir do retângulo central do boxplot. Eles são calculados da seguinte forma:
- Limite Inferior do Bigode: Q1 - 1,5 * (Q3 - Q1)
- Limite Superior do Bigode: Q3 + 1,5 * (Q3 - Q1)
-
Identificar Outliers: Os outliers são pontos que estão fora dos limites dos bigodes. Em outras palavras, qualquer ponto abaixo do limite inferior do bigode ou acima do limite superior do bigode é considerado um outlier.
Interpretação de um boxplot:
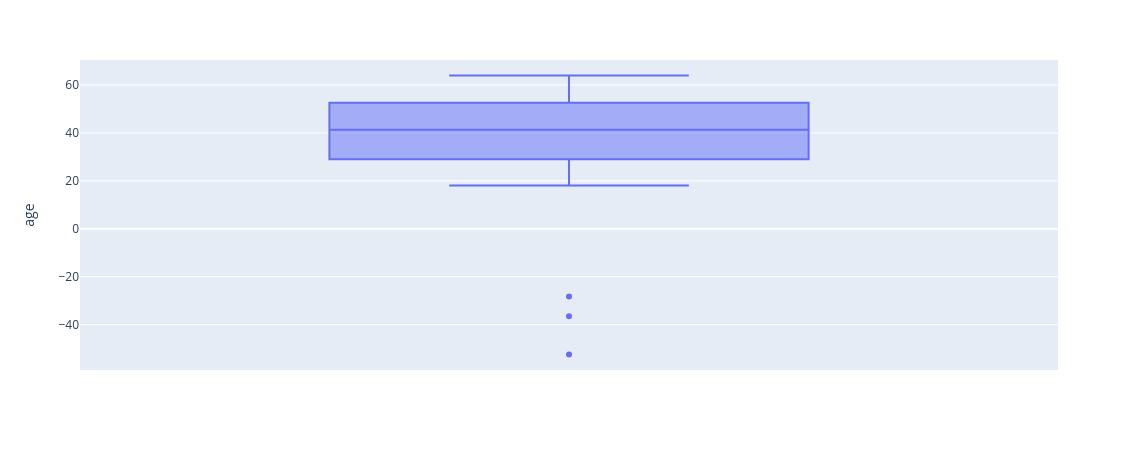
- O retângulo central representa o intervalo interquartil (IQR), que contém a maioria dos dados (50%).
- A linha dentro do retângulo representa a mediana (Q2), que divide o conjunto de dados ao meio.
- Os bigodes se estendem a partir do retângulo para fora até os valores mínimos e máximos dentro dos limites aceitáveis (1,5 vezes o IQR).
- Outliers são pontos individuais que estão além dos limites dos bigodes.
Identificação de outliers com um boxplot:
-
Outliers Inferiores: Qualquer ponto que esteja abaixo do limite inferior do bigode é um outlier inferior. Esses valores são considerados excepcionalmente baixos em relação à maioria dos dados.
-
Outliers Superiores: Qualquer ponto que esteja acima do limite superior do bigode é um outlier superior. Esses valores são considerados excepcionalmente altos em relação à maioria dos dados.
-
Outliers Extremos: Além dos outliers inferiores e superiores, os pontos que estão muito longe dos bigodes, geralmente a mais de 3 vezes o IQR, são considerados outliers extremos.
A principal vantagem do boxplot é que ele fornece uma representação visual clara da distribuição dos dados e torna os outliers facilmente identificáveis. Isso ajuda os analistas de dados a entender a natureza dos dados e a decidir como lidar com os outliers, seja removendo-os, investigando-os ou aplicando técnicas de tratamento específicas. Além disso, o boxplot é útil para comparar várias distribuições de dados e identificar discrepâncias entre elas.