Lista de adjacência
A ideia central é ter um vetor (ou array) principal, onde cada posição corresponde a um vértice do grafo. Nessa posição, em vez de um único valor, armazenamos uma lista de todos os outros vértices que são vizinhos daquele vértice.
Definição
A lista de adjacências de um grafo é um vetor chamado adj que contém listas, uma para cada vértice em .
Para cada vértice u, a lista adj[u] armazena todos os vértices v para os quais existe uma aresta {u, v}.
Exemplo
Para um grafo de 5 vértices, temos por exemplo:
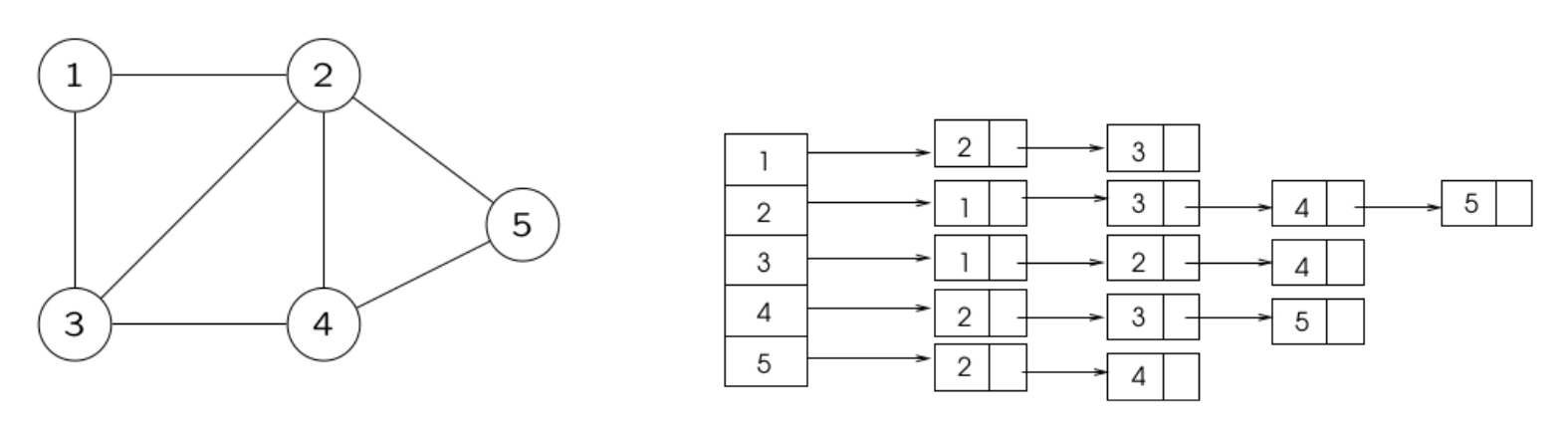
Análise
Vantagem: É uma representação mais econômica em termos de memória para grafos esparsos (grafos com poucas arestas em comparação com o número de vértices). O custo de memória é de .
Desvantagem: Verificar se existe uma aresta entre dois vértices específicos podem ser mais lento. No pior caso, pode ser necessário percorrer a lista inteira de vizinhos de um vértice, gerando o custo de