Intervalo de confiança
Resumo
O intervalo de confiança é um tipo de Inferência estatística que serve para estimar o valor de um parâmetro populacional.
O intervalo de confiança de nível C para um parâmetro corresponde a probabilidade de que o intervalo contenha o valor real do parâmetro em amostras repetidas. Em outras palavras, o nível de confiança é a taxa de sucesso do método.
O intervalo de confiança de 95% para uma média desconhecida (µ) é explicada, destacando o papel do valor “95%” na determinação desse intervalo. A construção do intervalo envolve encontrar os 95% centrais da distribuição amostral Normal, o que é feito afastando-se da média em duas vezes o desvio-padrão em ambas as direções.
A fórmula para construir intervalos de confiança é derivada a partir da distribuição amostral Normal, utilizando valores críticos, representados por
Os valores críticos desempenham um papel fundamental na determinação de quantos desvios-padrão nos afastamos da média em ambas as direções para capturar a porcentagem desejada da distribuição.
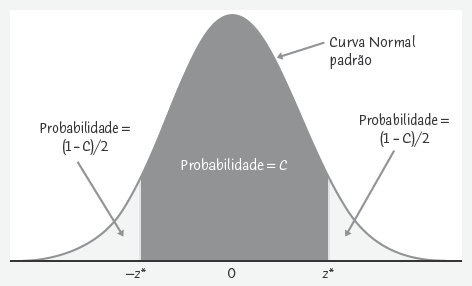A figura acima ilustra como a área central C sob a curva Normal padrão é delimitada pelos valores críticos
A probabilidade de valores C está entre
Extraia uma AAS de tamanho n de uma população Normal com média desconhecida µ e desvio-padrão conhecido σ. Um intervalo de confiança para µ de nível C é descrito por:
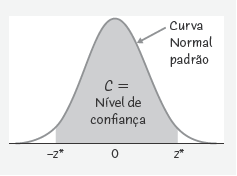
Essa abordagem fornece uma maneira sistemática de estabelecer intervalos de confiança para a média populacional com base na distribuição Normal padrão.