Portas lógicas §

---

George Boole foi o responsável por criar em 1948 um sistema matemático de análise lógica denominada de álgebra de Boole ou álgebra booleana. Esse sistema permitiu elaborar expressões lógicas que possibilitaram o desenvolvimento de circuitos digitais.

Introdução §

As portas lógicas são componentes básicos de decisão utilizados para criar circuitos digitais e integrados, desde níveis mais simples até complexos.

O funcionamento das portas lógicas consiste na verificação, em tempo de operação, os valores de entrada para determinar a saída.

Existem 7 tipos de portas lógicas:

• AND (“e”)
• OR (“ou”)
• NOT (“não”)
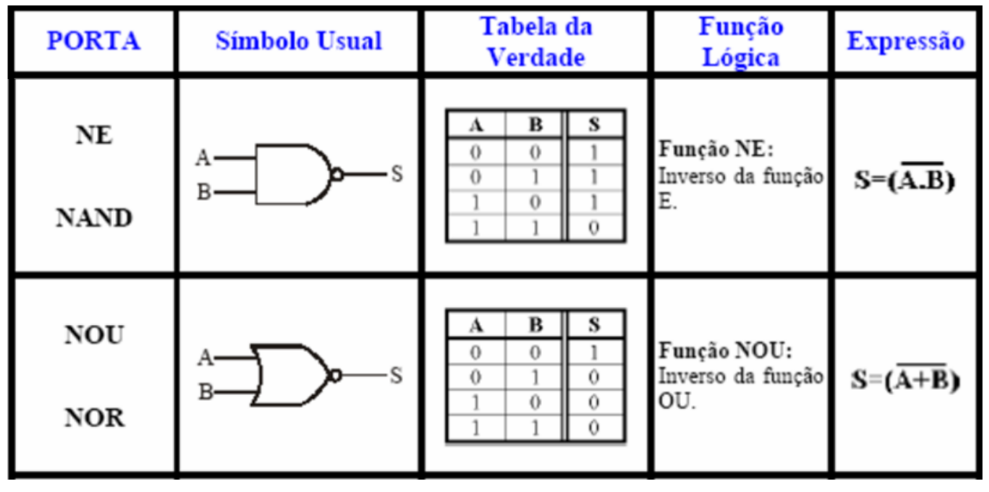
• NAND (“não e”)
• NOR (“não ou”)
• XOR (“ou exclusivo”)
• XNOR (“não ou exclusivo”)

Sendo que as portas AND, OR e NOT não os tipos fundamentais os quais derivaram as demais portas (NAND, NOR, XOR, XNOR).

As portas lógicas operam com níveis lógicos que representam o estado de entra ou saída de um circuito. O nível lógico é um representação que uma variável booleana pode assumir, por exemplo 0 ou 1.

• Nível lógico 0: pode representar falso, desligado, baixo, não, aberto, entre outros;
• Nível lógico 1: pode representar verdadeiro, ligado, alto, sim, fechado, entre outros.

Tabela verdade §

A tabela verdade é um mecanismo para descrever a relação entre a saída com os níveis lógicos de entrada de um circuito lógico.

A seguir um exemplo de tabela verdade para 2 variáveis de entrada e um saída:

Entrada A	Entrada B	Saída
0	0	0
0	1	0
1	0	0
1	1	1

Nessa tabela verdade:

• Quando ambas as entradas A e B são 0, a saída é 0.
• Quando uma das entradas é 0 e a outra é 1, a saída também é 0.
• Somente quando ambas as entradas A e B são 1, a saída é 1.

Note que a tabela verdade descreve todas as combinações possíveis de entradas do sistema e indica a saída para cada caso.

O circuito lógico representa um circuito lógico combinacional representado por portas lógicas combinadas ou individuais.

Circuitos combinacionais são aqueles em que o sinal de saída depende única e exclusivamente das combinações dos sinais de entrada. Os circuitos deste tipo não possuem nenhum tipo de memória, ou seja, as saídas não dependem de nenhum estado anterior do circuito.

Expressão booleana §

Uma expressão booleana, também conhecida como equação booleana, é uma representação lógica que descreve o comportamento da saída de um circuito com base nas variáveis de entrada. Seu propósito reside em elucidar a combinação das portas lógicas que constituem um sistema.

Por exemplo, considere um circuito lógico composto por duas entradas e uma saída. Nesse contexto, podem ser elaboradas as seguintes expressões lógicas:

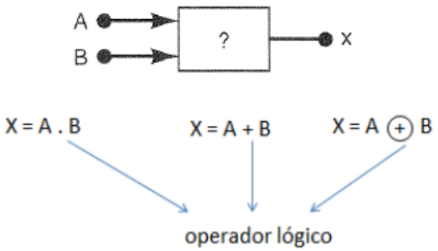
O tipo de operador lógico adotado determina a operação realizada nas entradas para resultar na saída correspondente.

Operação AND §

A porta lógica AND (“e”), representado por (ponto final), é constituída por duas entradas (“A”, “B”) e uma saída (“X”).

Simbologia:

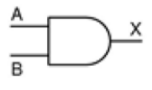
Expressão booleana:

Circuito elétrico equivalente:

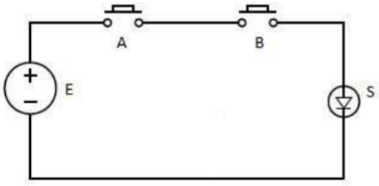
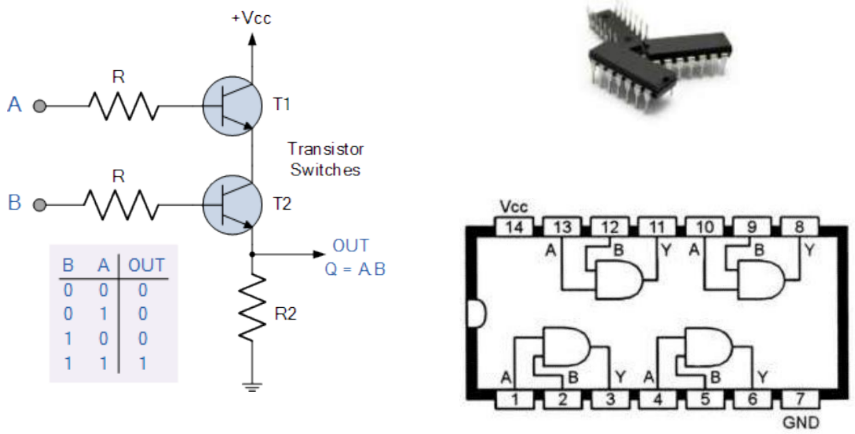
Comercialmente as portas são agregadas em circuitos integrados (CI). Por exemplo, o dispositivo integrado SN7408 de tecnologia TTL (Transistor-Transistor Logic) fabricado pela Texas Instruments (SN).

Operação OR §

A porta lógica OR (“ou”), representador por , é constituída por duas entradas (“A”, “B”) e uma saída (“X”).

Simbologia:

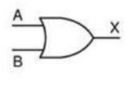
Expressão booleana:

Circuito elétrico equivalente:

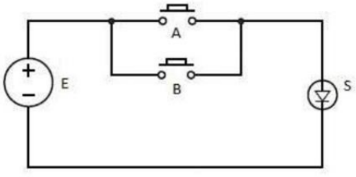
Comercialmente as portas são agregadas em circuitos integrados (CI). Por exemplo o dispositivo integrado SN7432 de tecnologia TTL (Transistor-Transistor Logic) fabricado pela Texas Instruments (SN).

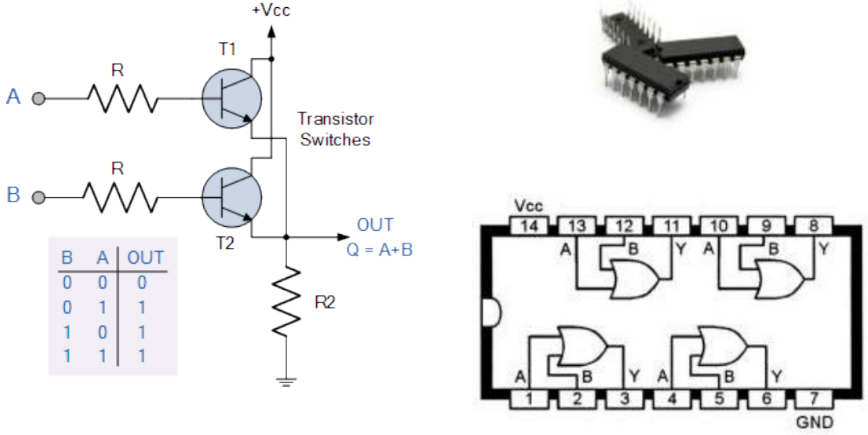
Operação NOT §

A porta lógica NOT (“não”), também chamado de porta lógica inversor, representado por (barra) ou (apóstrofe), é constituída de uma entrada (“A”) e uma saída (“X”).

Simbologia:

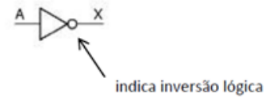
Expressão booleana:

Circuito elétrico equivalente:

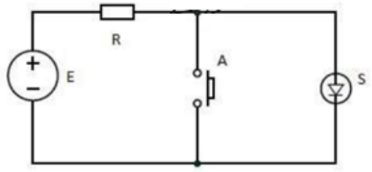
Comercialmente as portas são agregadas em circuitos integrados (CI). Por exemplo, o dispositivo integrado SN7404 de tecnologia TTL (Transistor-Transistor Logic) fabricado pela Texas Instruments (SN).

Buffer §

Buffer é uma porta lógica especial composta por duas portas inversoras que amplifica e reproduz um sinal de entrada sem inverter sua polaridade. Ele age como um repetidor de sinal, transmitindo o sinal de entrada diretamente para a saída, sem modificar sua natureza. O buffer é utilizado para reforçar o sinal, superando perdas devido a distâncias ou resistência.

Simbologia:

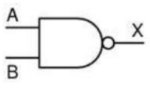
Operação NAND §

A porta lógica NAND (“não e”) é constituída de duas entradas (“A”, “B”) e uma saída (“X”).

Simbologia:

Expressão booleana:

Circuito elétrico equivalente:

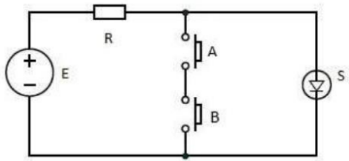
Comercialmente as portas são agregadas em circuitos integrados (CI). Por exemplo, o dispositivo integrado SN7400 de tecnologia TTL (Transistor-Transistor Logic) fabricado pela Texas Instruments (SN).

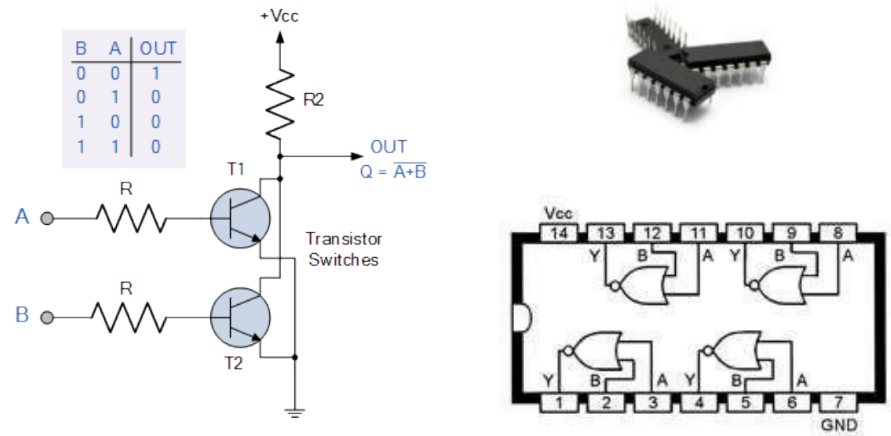
Operação NOR §

A porta lógica NOR (“não ou”) é constituída de duas entradas (“A”, “B”) e uma saída (“X”).

Simbologia:

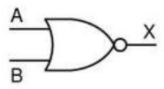
Expressão booleana:

Circuito elétrico equivalente:

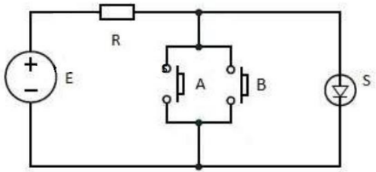
Comercialmente as portas são agregadas em circuitos integrados (CI). Por exemplo, o dispositivo integrado SN7402 de tecnologia TTL (Transistor-Transistor Logic) fabricado pela Texas Instruments (SN).

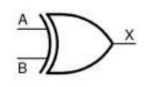
Operação XOR §

A porta lógica XOR (“ou exclusivo”), representado por , é constituída de duas entradas (“A”, “B”) e uma saída (“X”).

Simbologia:

Expressão booleana:

Circuito elétrico equivalente:

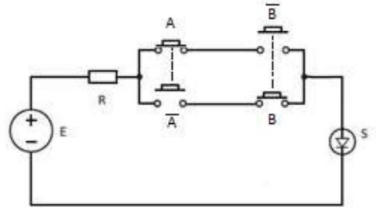
Comercialmente as portas são agregadas em circuitos integrados (CI). Por exemplo, o dispositivo integrado SN7486 de tecnologia TTL (Transistor-Transistor Logic) fabricado pela Texas Instruments (SN).

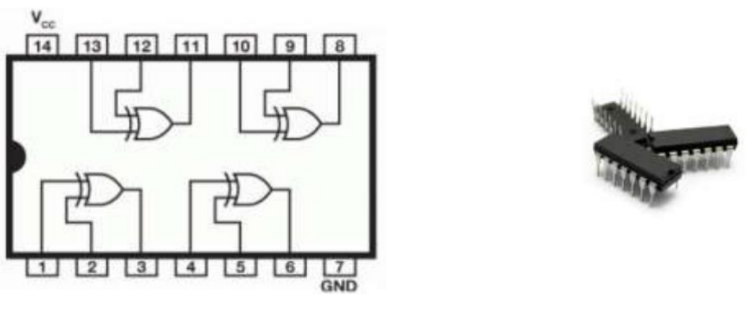
Operação XNOR §

porta lógica XNOR (“não ou exclusivo”), representado por , é constituída de duas entradas (“A”, “B”) e uma saída (“X”).

Simbologia:

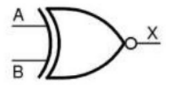
Expressão booleana:

Circuito elétrico equivalente:

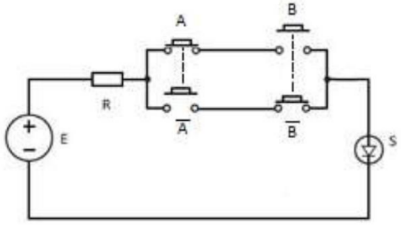
Comercialmente as portas são agregadas em circuitos integrados (CI). Por exemplo, o dispositivo integrado SN74266 de tecnologia TTL (Transistor-Transistor Logic) fabricado pela Texas Instruments (SN).

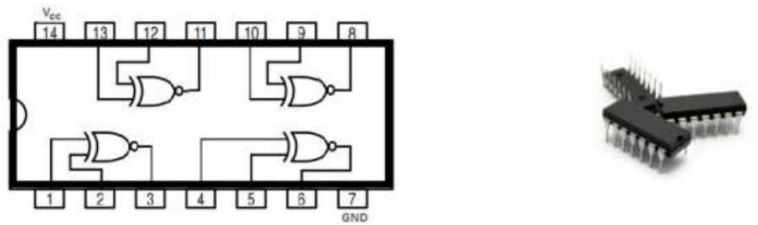
Resumo portas lógicas §

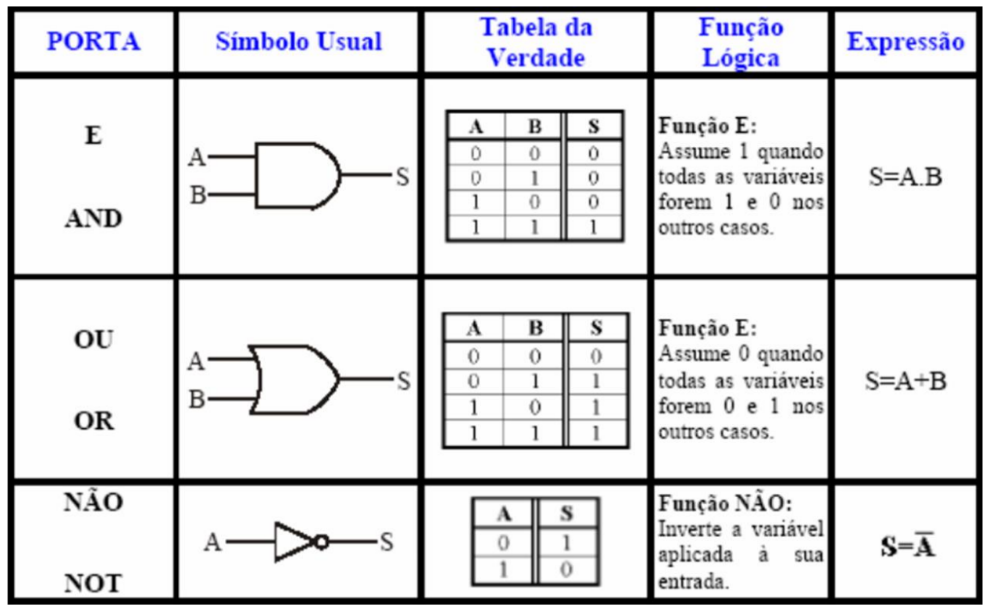
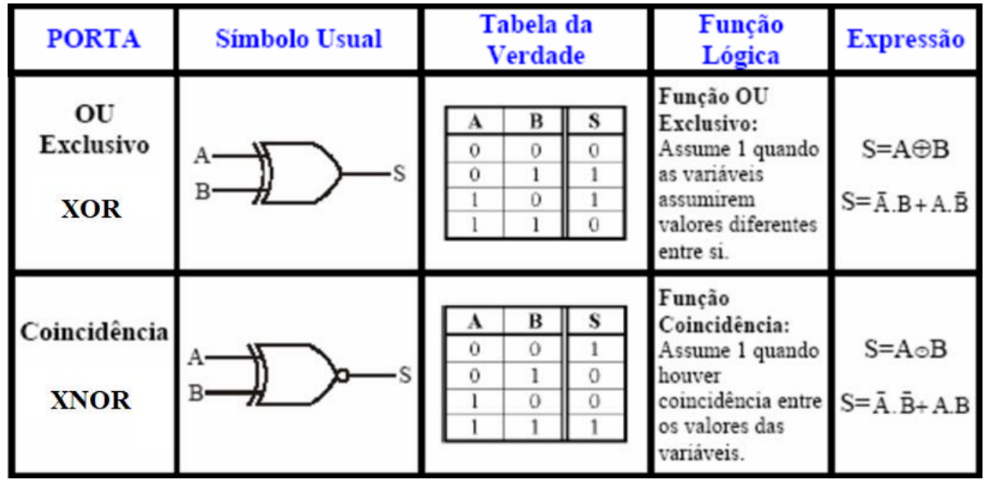
Aplicações porta lógica XOR §

A porta XOR é amplamente empregada em circuitos de meio somador e somador completo, especialmente para realizar adições binárias. Nos circuitos de somador, a porta XOR desempenha um papel fundamental.

O circuito de meio somador utiliza portas XOR para combinar duas entradas binárias e produzir a saída de soma, enquanto uma porta AND é utilizada para gerar o carry (vai-um). Através da tabela verdade, podemos verificar que os três primeiros resultados estão em conformidade com as regras da adição binária. Quando ambos os bits de entrada são 1, a porta XOR gera uma saída 0 e a porta AND produz um carry 1, garantindo a lógica de soma.

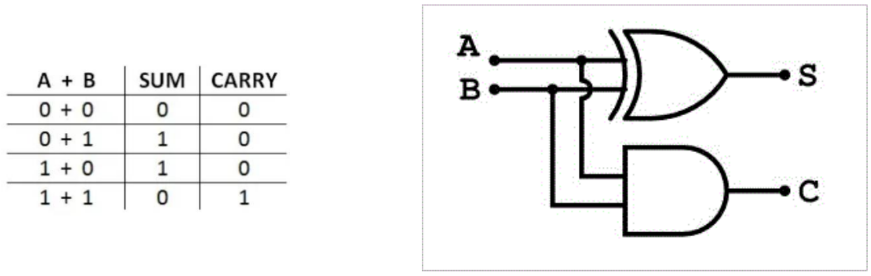
O somador completo, por sua vez, expande o meio somador ao incluir um bit de carry de entrada. Aqui, a porta XOR é empregada para somar as entradas binárias juntamente com o carry de entrada, e as portas AND são utilizadas para calcular os carries de saída e entrada para o próximo estágio.

Além das aplicações em circuitos de somadores, a porta XOR também desempenha um papel crucial em circuitos de geração e checagem de paridade.

A checagem de paridade é uma técnica usada para detectar erros em dados transmitidos, especialmente em comunicações digitais. Um bit de paridade é adicionado aos dados para garantir que o número total de bits de valor 1 seja sempre par ou ímpar. Isso ajuda a identificar erros de transmissão.

A porta XOR é utilizada nesse contexto para calcular o bit de paridade. Ao analisar os bits de entrada e gerar uma saída 1 sempre que houver um número ímpar de bits de valor 1, ela cria um padrão que pode ser comparado ao bit de paridade recebido após a transmissão. Se os padrões não corresponderem, isso indica a presença de um erro na transmissão dos dados.

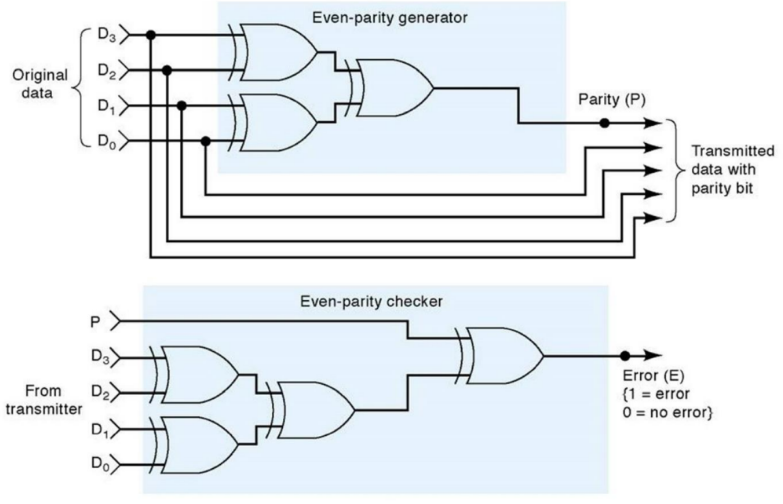
Dessa forma, a porta XOR é usada para calcular e verificar o bit de paridade, desempenhando um papel essencial nos circuitos de checagem de paridade. Isso garante a detecção confiável de erros de transmissão em sistemas digitais.

Equivalência de portas lógicas §

A equivalência de portas lógicas refere-se à capacidade de criar uma mesma função booleana utilizando diferentes combinações de portas lógicas. Em outras palavras, dois ou mais circuitos são considerados equivalentes quando ambos realizam a mesma operação lógica, mesmo que sejam construídos com diferentes tipos de portas.

A criação de funções booleanas equivalentes a partir de diferentes portas lógicas é uma técnica comum na otimização de circuitos digitais. Ela permite encontrar alternativas mais eficientes em termos de consumo de recursos, como espaço e energia.

Funções lógicas equivalentes a partir de portas AND e NOT:

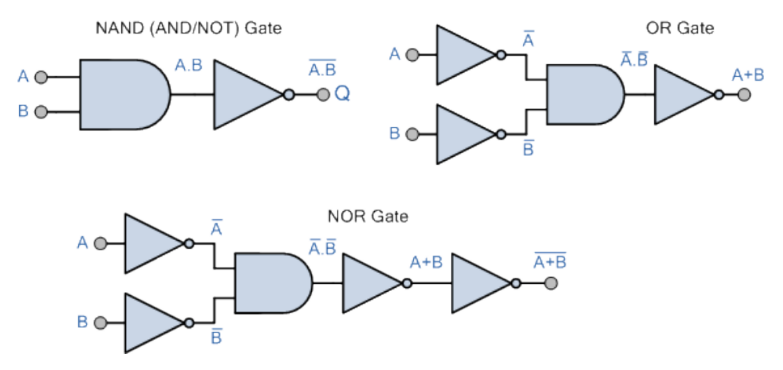
Funções lógicas equivalentes a partir de portas OR e NOT:

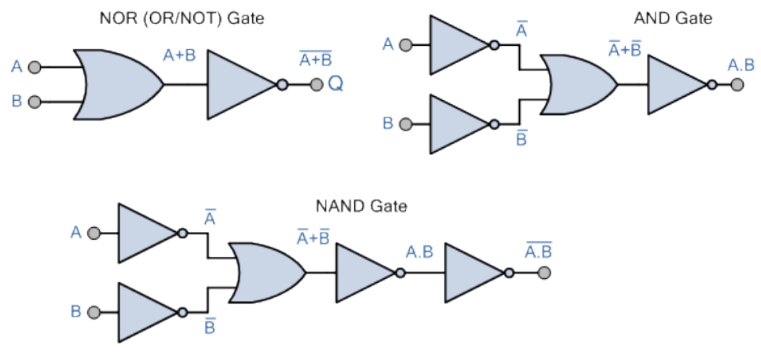
Portas lógicas universais NAND e NOR §

As portas lógicas universais NAND (“não e”) e NOR (“não ou”) são componentes fundamentais na construção de circuitos digitais, pois são capazes de implementar qualquer função lógica utilizando combinações delas. Essa propriedade de universalidade as tornam importantes na construção de circuitos digitais complexos.

Porta lógica NAND:

A porta lógica NAND possui duas ou mais entradas e uma única saída. Ela retorna o resultado “falso” (0) apenas quando todas as entradas são verdadeiras (1).

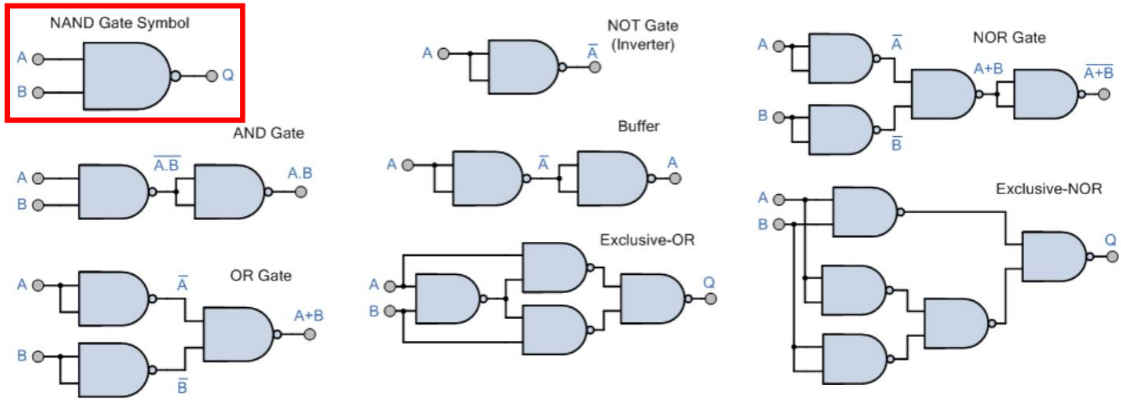
Sua função é equivalente à negação da porta lógica AND (“e”) em todas as suas entradas. A principal propriedade da porta NAND é que ela pode ser usada para implementar outras portas lógicas, como NOT, AND e OR. Isso ocorre porque a combinação correta de portas NAND pode reproduzir as operações dessas portas.

Porta lógica NOR:

A porta lógica NOR também possui duas ou mais entradas e uma única saída. Ela retorna o resultado “verdadeiro” (1) apenas quando todas as entradas são falsas (0).

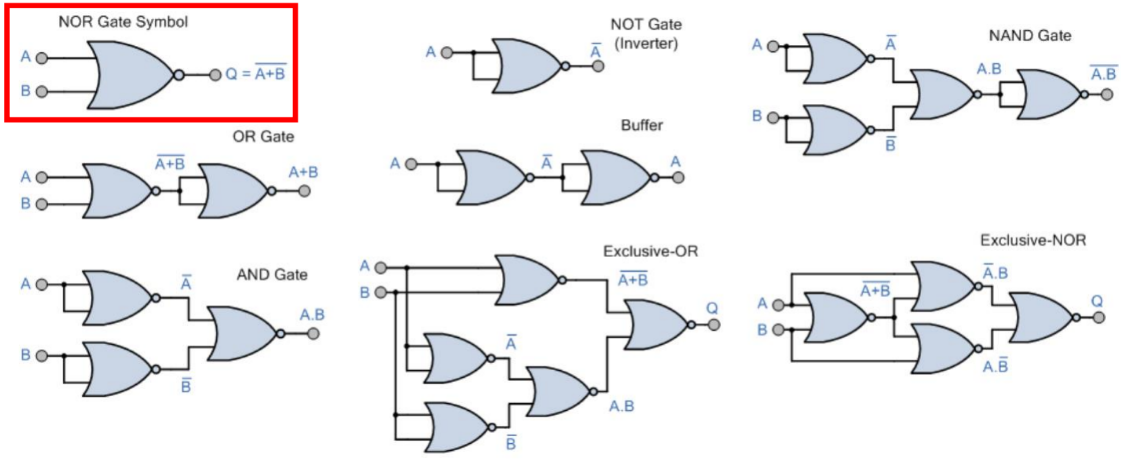
Sua função é equivalente à negação da porta lógica OR (“ou”) em todas as suas entradas. Da mesma forma que a porta NAND, a porta NOR pode ser usada para implementar outras portas lógicas, tornando-se universal.

Descrição algébrica de circuitos lógicos §

A descrição algébrica de circuitos lógicos é uma abordagem que utiliza operações booleanas com os operadores AND, OR e NOT para representar circuitos digitais complexos construídos a partir de duas ou mais portas lógicas. Essa representação permite uma análise e síntese mais compreensíveis dos circuitos, além de possibilitar a comparação direta com expressões lógicas equivalentes.

Por exemplo, considerando o circuito lógico apresentado acima, a expressão algébrica equivalente é dada por ou , com a operação AND possuindo precedência sobre a operação OR. No entanto, essa ordem de operações pode ser modificada com o uso de parênteses, como em , que indica que a operação OR é executada primeiro.

A representação algébrica também envolve o uso de inversores, onde a expressão da saída é a expressão de entrada com uma barra sobre ela, indicando a inversão. Essa representação pode ser alternativamente feita com o uso do sinal de apóstrofo (').

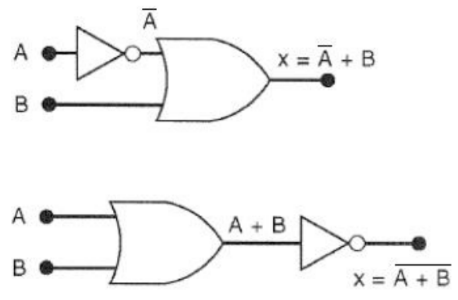
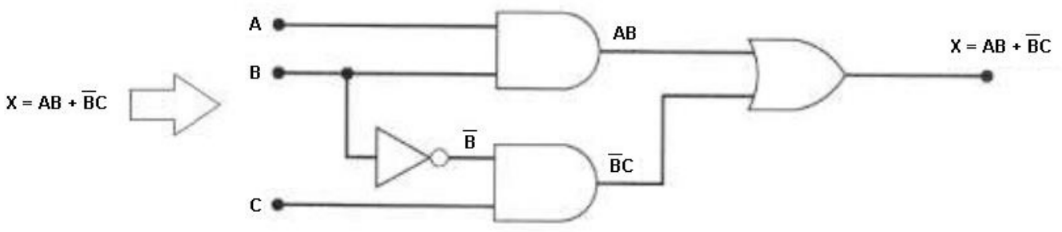
Além disso, a descrição algébrica permite descrever um circuito lógico a partir da sua expressão lógica correspondente. Por exemplo, se a expressão lógica é , os termos e são entradas de uma porta OR e podem ser gerados por portas AND.

Essa dualidade também permite obter uma expressão lógica a partir de um circuito lógico, ou vice-versa. Por exemplo:

Do circuito lógico:

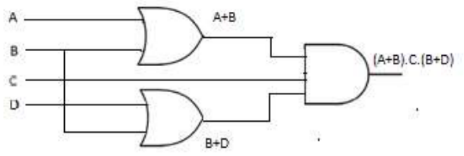
Obtém-se a expressão lógico:

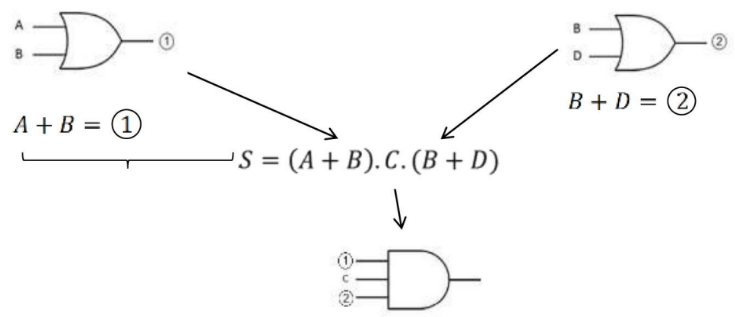
Em resumo, a descrição algébrica de circuitos lógicos é uma técnica valiosa para analisar, projetar e compreender circuitos digitais complexos, permitindo a representação desses circuitos em termos de operações booleanas e expressões lógicas equivalentes.

Teoremas §

A definição matemática de um teorema se refere a uma proposição que pode ser comprovada por meio de um processo lógico. Essa mesma lógica se estende à álgebra booleana, onde regras e teoremas booleanos são aplicados para simplificar as expressões em circuitos lógicos, resultando em implementações otimizadas.

Teorema da complementação §

O teorema booleano da complementação estabelece que o complemento de é representado por . Portanto, podemos estabelecer a identidade por meio da complementação.

Se , então , e, consequentemente, .

Por outro lado, se , então , e, nesse caso, .

Teorema da adição §

O teorema da adição na álgebra booleana estabelece as seguintes regras:

1. Identidade ou elemento nulo: Adicionar uma variável a um nível lógico 0 resultará no valor da própria variável.

2. Aniquilação ou elemento unitário: Adicionar uma variável a um nível lógico 1 sempre resultará no valor lógico 1.

3. Idempotência: Adicionar uma variável a si mesma resultará na própria variável.

4. Complementariedade: Adicionar uma variável ao seu complemento resultará no valor lógico 1.

Teorema da multiplicação §

O teorema da multiplicação na álgebra booleana estabelece as seguintes regras:

1. Aniquilação ou elemento unitário: Multiplicar uma variável a um nível lógico 0 sempre resultará no valor lógico 0.

2. Identidade ou elemento nulo: Multiplicar uma variável a um nível lógico 1 resultará no valor da própria variável.

3. Idempotência: Multiplicar uma variável a si mesma resultará na própria variável.

4. Complementariedade: Multiplicar uma variável ao seu complemento resultará no valor lógico 0.

Propriedades matemáticas §

1. Comutativa:

2. Associativa:

3. Distributiva:

4. Absorção ou cobertura:

5. Eliminação:

6. Eliminação:

7. Consenso ou fantasma:

8. Conversão;

Teoremas de De Morgan §

Augustus De Morgan (1806 a 1871) foi um matemático responsável pela elaboração das leis de De Morgan e também foi o primeiro a introduzir a ideia de indução matemática.

A indução matemática é um método de prova matemática usada para demonstrar a verdade de um número infinito de proposições.

1. 1º Teorema de De Morgan: o complemento do produto é igual a soma dos complementos.

   

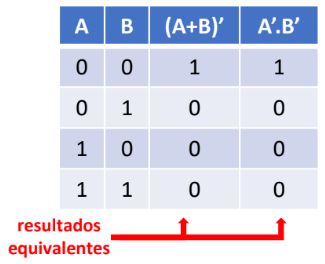
2. 2º Teorema de De Morgan: o complemento da soma é igual ao produto dos complementos

   

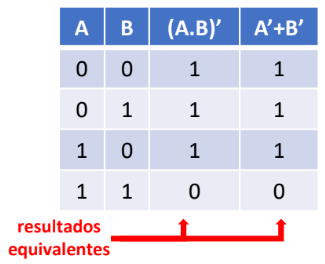
Expressão dual §

Uma expressão dual, na Álgebra de Boole, é uma expressão que mantém sua validade quando você troca os operadores lógicos AND e OR, bem como quando você inverte 0s e 1s. O Princípio da Dualidade afirma que qualquer igualdade algébrica derivada desses axiomas sempre será válida.

Para obter a expressão dual de uma expressão original, você deve seguir este procedimento:

1. Troque os operadores de multiplicação () por adição () e vice-versa.
2. Troque 0s por 1s e 1s por 0s.
3. Mantenha as prioridades da expressão original, adicionando ou removendo parênteses conforme necessário.

Isso significa que, se você tiver uma expressão booleana, poderá obter sua expressão dual aplicando essas transformações. Essa dualidade é útil para simplificar expressões e encontrar formas equivalentes de representar circuitos lógicos.

Por exemplo:

• Se você tiver a expressão original , sua expressão dual, , será .

• Se você tiver a expressão original , sua expressão dual, , será .

De acordo com o Princípio da Dualidade, as expressões originais e suas expressões duais permanecem válidas, mas isso não implica que ou que . No entanto, ambas as expressões representam a mesma lógica de forma equivalente.

O Princípio da Dualidade também é aplicado nas igualdades algébricas para a dedução de novas expressões a partir de teoremas existentes, permitindo explorar essa dualidade para simplificar e derivar novas expressões lógicas:

• Consenso ou fantasma:

  expressão dual

• Conversão;

  expressão dual

Expressão complementar §

Uma expressão complementar em álgebra booleana é uma forma de obter o valor complementar ou negado da expressão original. Para se criar a expressão complementar, você deve seguir este procedimento:

1. Trocar os operadores de multiplicação () por adição () e vice-versa.
2. Trocar os valores lógicos 0 por 1 e vice-versa.
3. Complementar todas as variáveis, ou seja, inverter o valor de cada variável (0 para 1 e 1 para 0).

Assim como na expressão dual, as prioridades da expressão original são mantidas pela adição ou remoção de parênteses.

A expressão complementar se baseia no Princípio da Dualidade, mas com a adição da complementação de todas as variáveis. Isso significa que, além de trocar operadores e valores lógicos, você também inverte todos os valores das variáveis na expressão.

Para ilustrar, aqui estão alguns exemplos de expressões e suas expressões complementares:

1. Expressão original: Expressão complementar:

2. Expressão original: Expressão complementar:

É importante observar que a expressão complementar é sempre o inverso da expressão original. Por exemplo, o complementar de é , e o complementar de é . Isso significa que, quando uma variável é verdadeira na expressão original, ela se torna falsa na expressão complementar e vice-versa. Essa técnica é frequentemente usada para simplificar e manipular expressões lógicas em álgebra booleana.

Referências §

---