Regressão
Reta de regressão
A regressão linear envolve a construção de uma reta de regressão que melhor descreve a relação entre duas variáveis, geralmente chamadas de variável explicativa (x) e variável de resposta (y). A reta de regressão é uma representação visual dessa relação e é extremamente útil para prever como o valor de y se comporta à medida que x varia.
A reta de regressão é definida pela fórmula matemática:
Onde:
- é o intercepto, que representa o valor estimado de quando .
- é o coeficiente de inclinação, descreve a taxa da variação de à medida que aumenta em uma unidade.
No entanto, é importante destacar que a regressão linear é apropriada apenas para problemas em que a relação entre x e y é linear (problemas linearmente separados), ou seja, quando os dados podem ser aproximados por uma linha reta. Quando essa suposição é atendida, a reta de regressão se torna uma ferramenta poderosa para modelar e entender a relação entre as variáveis.
Reta de regressão de mínimo quadrados
A reta de regressão de mínimos quadrados é uma técnica fundamental em análise estatística que busca encontrar a melhor reta para representar a relação entre duas variáveis, geralmente chamadas de variável independente (x) e variável dependente (y). Essa reta é chamada de “reta de regressão” porque é usada para prever ou estimar os valores da variável dependente com base nos valores da variável independente.
A ideia principal por trás da reta de regressão de mínimos quadrados é minimizar a soma dos quadrados dos erros residuais. Os erros residuais são as diferenças entre os valores observados (reais) da variável dependente e os valores previstos pela reta de regressão. O objetivo é ajustar a reta de tal forma que essa soma dos quadrados dos erros seja a menor possível, daí o nome “mínimos quadrados”.
A equação geral da reta de regressão é:
Onde:
- é a variável dependente (a que queremos prever).
- é a variável independente (a que usamos para fazer a previsão).
- é o intercepto da reta, que representa o valor de quando é igual a zero.
- é o coeficiente de inclinação da reta, que descreve a taxa de mudança em para uma mudança unitária em .
Para encontrar os valores de e que minimizam a soma dos quadrados dos erros residuais, são aplicadas técnicas de cálculo diferencial e otimização. Aqui estão os principais passos para calcular a reta de regressão de mínimos quadrados:
-
Calcule as médias de e , denotadas como e , respectivamente.
-
Calcule o coeficiente de correlação linear entre e . O coeficiente de correlação mede a força e a direção da relação linear entre as duas variáveis.
-
Cálculo do coeficiente de correlação de Pearson
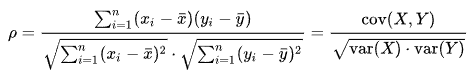
- : é a covariância de e , ou seja, a variância de e , matematicamente é representado por , pois o conectivo “e” têm função de multiplicação, como a Teoria Fundamental da Contagem.
-
Calcule o coeficiente de inclinação da reta de regressão usando a fórmula:
Onde:
- é o desvio padrão de .
- é o desvio padrão de .
- é o coeficiente de correlação entre as variáveis e .
-
Calcule o intercepto da reta de regressão usando a fórmula:
Agora com os valores de e que definem a reta de regressão de mínimos quadrados, é possível representar a melhor aproximação linear para a relação entre e de acordo com o critério de mínimos quadrados.
A reta de regressão de mínimos quadrados é amplamente utilizada em análise de dados e previsão, pois fornece uma maneira objetiva e matematicamente sólida de modelar a relação entre duas variáveis. É uma ferramenta fundamental em estatística e análise de regressão.