Relações discretas §

---

A definição formal de relações discreta é muito similar com o conceito intuitivo. Alguns exemplos intuitivos sobre relações:

• Parentesco
• maior ou igual (como estatura de pessoas)
• igualdade (como de número reais)
• faz fronteira com (para países)
• fila de pessoas para um caixa do supermercado
• banco de dados relacional

Além disso, a relação também é aplicável na matemática, assim como na computação:

• Teoria de conjuntos (igualdade e continência)
• Lógica (equivalência e implicância)

As relações descritas acima, são consideradas binárias, pois são operações que envolvem sempre dois elementos. Dessa forma, existem relações que envolvem mais de dois elementos, como por exemplo relações ternárias, quaternárias.

Produto cartesiano §

A definição do produto cartesiano é a seguinte:

Dados dois conjuntos, A e B, definimos o produto cartesiano entre eles, representado por , como o conjunto:

Essencialmente, o produto cartesiano é o conjunto de todos os possíveis pares de elementos que podem ser formados entre os conjuntos A e B. É importante observar que, embora a definição inicial envolva apenas dois conjuntos, o conceito do produto cartesiano pode ser estendido para mais conjuntos. A forma generalizada do produto cartesiano é:

Relação §

Relação binária e N-ária §

Uma relação binária entre dois conjuntos e é representada como um subconjunto do produto cartesiano , ou seja:

No contexto de uma relação binária, é chamado de domínio da relação, enquanto é chamado de contradomínio (ou condomínio).

Analogamente, podemos definir uma relação n-ária. Uma relação n-ária sobre é um subconjunto do produto cartesiano generalizado :

Quando o conjunto subjacente à relação é discreto (ou seja, finito ou enumerável), nos referimos a como uma relação discreta.

Exemplos de relações §

Considere os conjuntos , e . Aqui estão alguns exemplos de relações:

a) é uma relação de para , assim como de para , de para , etc. Isso ocorre porque o conjunto vazio é um subconjunto de qualquer conjunto.

b) é uma relação que parte de e chega em (pois ).

c) Dentro do conjunto de partida e o conjunto de chegada , a relação de igualdade é .

d) representa a relação “menor que” de em .

e) é uma relação de para .

Uma relação também pode ser denotada como , e frequentemente um elemento é representado de forma infixada como .

Endorrelação ou Auto-relação §

Suponha seja um conjunto. Nesse contexto, uma relação (com origem e destino no mesmo conjunto) é chamada de endorrelação ou auto-relação. Nesse caso, afirmamos que é uma relação em .

Uma endorrelação é frequentemente representada como <>.

a) <>:

Neste exemplo, temos o conjunto dos números naturais como o conjunto base. A relação <> denota uma endorrelação em , onde representa a relação “menor ou igual a”. Em outras palavras, para cada par de elementos e em , a relação <> inclui o par ordenado se for menor ou igual a .

Por exemplo, se e , então pertence a <> porque é menor que . Portanto, esta endorrelação representa a relação “ser menor ou igual a” entre os números naturais.

b) <>:

Neste exemplo, representa o conjunto dos números inteiros, e a relação <> é uma endorrelação em . No entanto, denota o conjunto vazio de pares ordenados, o que significa que esta endorrelação não inclui nenhum par ordenado. Portanto, em termos práticos, não representa nenhuma relação entre os números inteiros. Pode-se dizer que esta endorrelação é “vazia” ou não contém elementos.

c) <>:

Neste exemplo, representa o conjunto dos números racionais. A relação <> é uma endorrelação em que usa o operador ”=” para denotar a relação de igualdade. Isso significa que, para qualquer número racional em , o par ordenado pertence a <>, porque um número sempre é igual a ele mesmo.

Exercício 1 §

Considere novamente os conjuntos e . Construa uma relação binária entre estes dois conjuntos e, posteriormente, represente, no mesmo plano cartesiano abaixo, o produto cartesiano e a relação :

Exercício 2 §

Seja o conjunto .

a) Obtenha o produto cartesiano de . b) Obtenha os elementos (pares) da relação , ou . c) Obtenha os elementos (pares) da relação ou d) Obtenha os elementos (pares) da relação ou

Exercício 3 §

Sejam e . Para cada uma das seguintes relações: ▪ explicite os elementos (pares) da relação; ▪ determine o domínio da função; ▪ determine o conjunto imagem.

a)

b)

c)

d)

e)

Propriedade de endorrelação §

Além das propriedades definidas nas relações genéricas, existem outras como:

• Reflexividade
• Simetria
• Transitividade

Reflexividade §

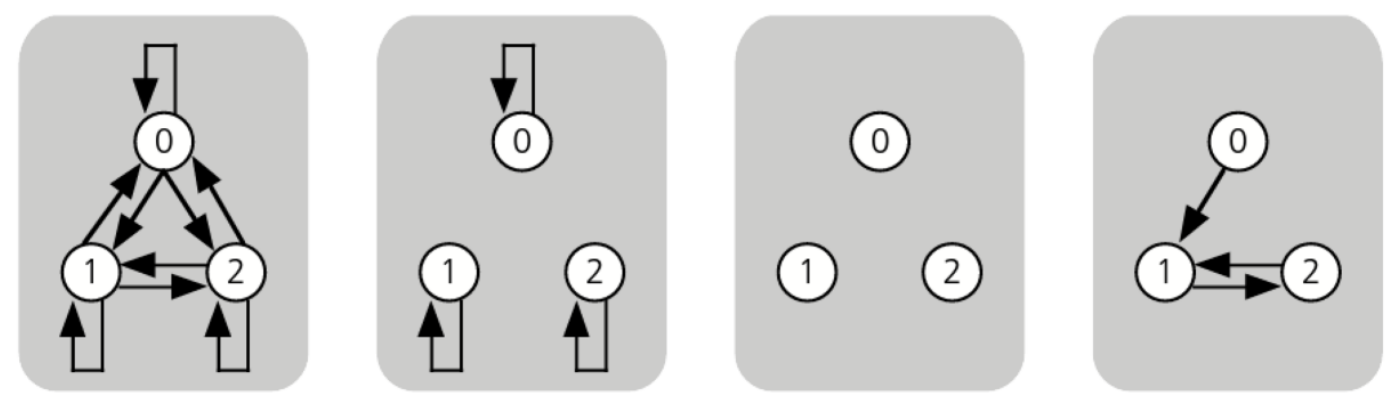
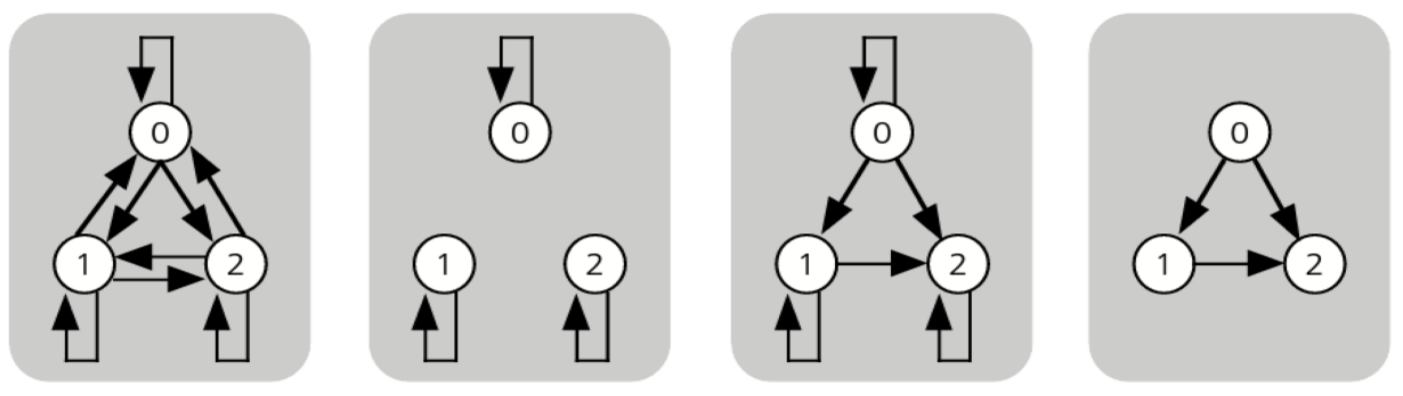
Dizemos que uma endorrelação é reflexiva se somente se todos os elementos de estiver relacionado consigo mesmo, ou seja, . Na representação matricial, basta que todos os elementos da diagonal principal seja 1 para que a endorrelação seja reflexiva, como pode ser observado nas matrizes e . Já em grafos, a endorrelação é reflexiva quando a flecha tem a origem e destino no próprio nó, como acontence nos grafos 1 e 2.

Simetria §

Dizemos que uma endorrelação é simétrica se somente se . Na representação matricial, a simetria é em relação a diagonal principal, como é possível visualizar nas matrizes e . 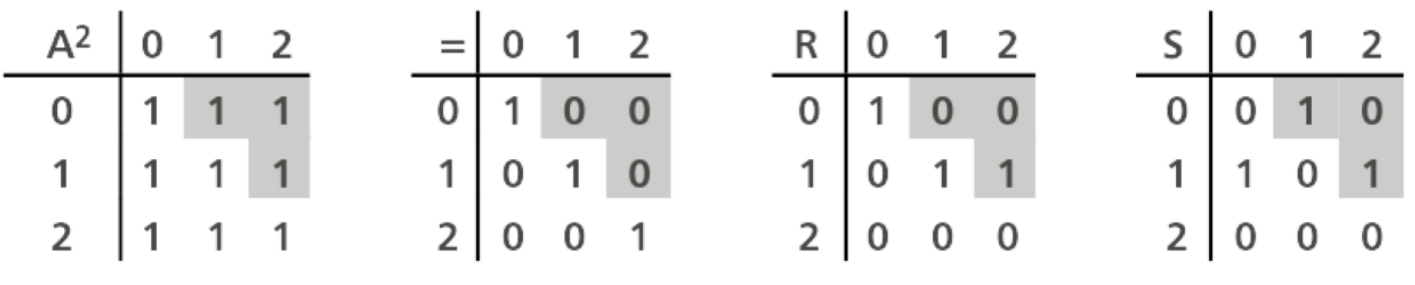Já em grafos, essa propriedade é representada quando uma dada fecha vai do nó 0 ao 1, exista uma outra fecha que faça o caminho inverso (do nó 1 ao 0), isso acontece nos grafos 1 e 2.

Transitividade §

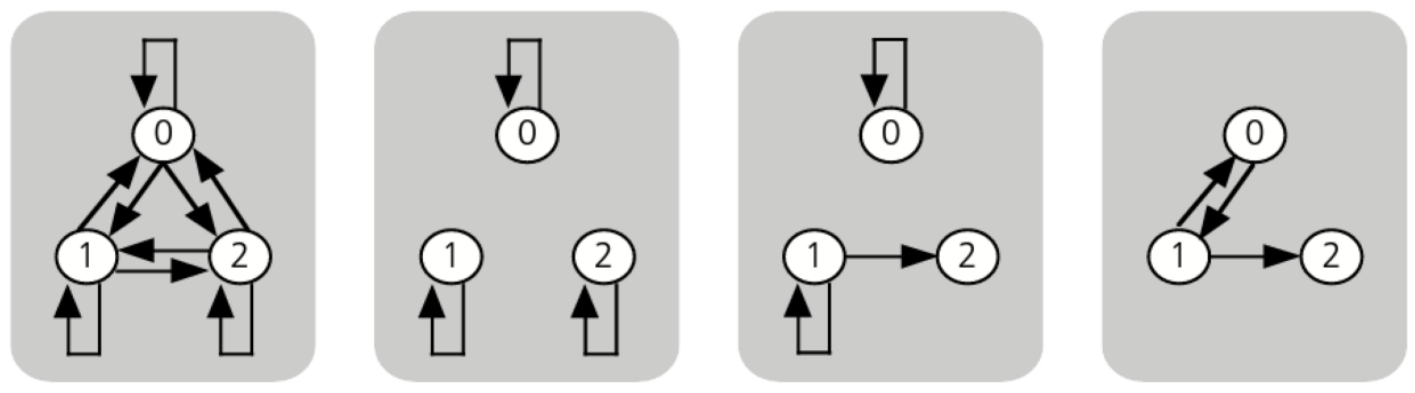
Dizemos que uma endorrelação se somente se . Na representação matricial, a endorrelação é transitiva quando para um caminho alternativo (longo), necessariamente há uma caminho atalho (curto). Já em grafos, a visualização da transitividade é mais fácil do que em matrizes. Na figura abaixo, os grafos 1, 3 e 4 representam uma endorrelação transitiva.

Fecho de um endorrelação §

Em alguns cenários, é desejado estender uma endorrelação de tal forma que esta extensão satisfaça um determinado conjunto de propriedades . A menor relação que contenha e que satisfaça é chamado de fecho de R em relação a P, denotado por .

Existem 4 fechos importantes para endorrelação:

• Fecho reflexivo:
• Fecho simétrico:
• Fecho transitivo ()
  • Se , então
  • e , então
• Fecho reflexivo-transitivo ()

Relação de equivalência §

A relação de equivalência explica a igualdade semântica, em outras palavras, quando entidades sintaticamente diferentes podem ser equivalentes segundo uma relação.

Por exemplo, números pares podem ser reunidos num mesmo grupo. Todo Ela consiste em dois element s os números que pertencem a este grupo compartilham a mesma propriedade: são pares. Ou seja, estão relacionados por serem números pares. Os números 2 e 4, por exemplo, são sintaticamente diferentes (como números). Porém, são semanticamente iguais quando consideramos a propriedade de serem números pares.

Note

A relação de equivalência é amplamente utilizado na computação, por exemplo em orientação a objetos.

Para que um endorrelação seja uma relação de equivalência, ela precisa ter as seguintes propriedades:

• Ser reflexiva
• Ser transitiva
• Ser simétrica

Relações de equivalência implicam em partições nos conjuntos onde são definidas. Cada uma destas partições é chamada de classe de equivalência. Uma classe de equivalência é representada por ou , onde é um representante da classe de equivalência. A definição formal disso é:

Aplicação: análise orientada a objetos §

Ao adotarmos o paradigma orientado a objeto para analisar um domínio, procuramos classificar os objetos deste domínio dentro de conjuntos chamados classes. Uma classe agrupa objetos com atributos e comportamentos iguais. Dessa forma, essa igualdade de atributos e comportamentos é uma representação da relação de equivalência. Baseado na seguinte proposição:

Dois objetos e pertencem a uma classe e têm atributos e comportamentos iguais.

Logo dizemos que se trata de uma relação de equivalência, pois cada classe identificada no domínio é uma classe de equivalência.

Relações de ordem §

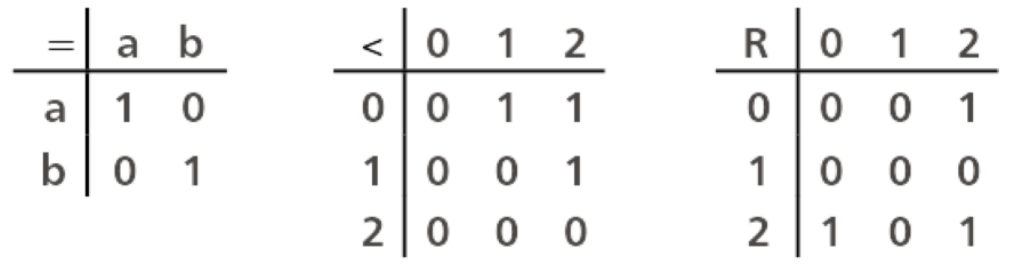
Em alguns cenários, como as relações de ordem, é preferível que a inversão de um par relacionado não esteja presente na relação, ou seja, se então . Isso caracteriza a propriedade antissimétrica.

Uma endorrelação é antissimétrica se e somente se .

Por definição, a única simetria permitida em uma relação antissimétrica é a reflexiva.

Uma endorrelação é uma relação de ordem parcial se e somente se ela tiver as seguintes propriedade:

• Reflexividade
• Antissimetria
• Transitividade

Normalmente a representação de uma relação de ordem parcial é feito pelo símbolo e dizemos que é um c.p.o. (conjunto parcial ordenado). Se a relação for total, então se trata de uma relação de ordem total e é um c.t.o. (conjunto totalmente ordenado).

A notação permite reescrever uma relação de ordem num conjunto da seguinte forma:

• (propriedade reflexiva)
• Se e , então (propriedade antissimétrica)
• Se e então (propriedade transitiva)

Aplicação: ordenação de tipos §

Conjuntos parcialmente ordenados (c.p.o) é amplamente utilizado na computação, por exemplo na Teoria de Tipos.

Suponha o seguinte diagrama de classes para representar uma aplicação de c.p.o. na computação: 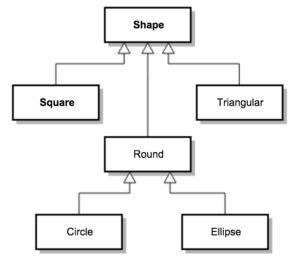O mecanismo de herança pode ser visto como uma inclusão de conjuntos e pode ser organizado na seguinte ordem:

• Shape Square
• Shape Round Circle
• Shape Round Ellipse
• Shape Triangular

Com base nestas ordens, e com as propriedades reflexiva e transitiva, podemos representá-las da seguinte forma com Java.

Shape s = new Shape();
Shape r = new Round();
Shape c = new Circle();
Round e = new Ellipse();

Esse mecanismo é chamado de covariância de tipos em um linguagem de programação e está relacionado com a ordenação de tipos como conjuntos.

Diagrama de Hasse §

O diagrama de Hasse é uma maneira simplificada de representar uma relação de ordem parcial a partir de um número mínimo de setas para representá-la em um grafo orientado. Isso só é possível pelo fato de um c.p.o. ser um fecho reflexivo-transitivo, responsáveis pela dedução das flechas omitidas.

Por exemplo, dado um conjunto tal que e temos um c.p.o. ():

Então podemos representar essa relação usando um grafo orientado convencional 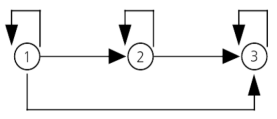Ou por meio do Diagrama de Hasse 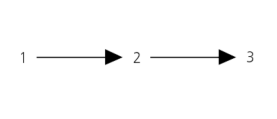Alternativamente, o Diagrama de Hasse acima pode ser representado sem as setas, numa posição vertical. 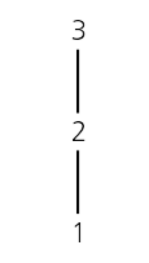Na figura acima, os menores elementos da relação ocupa a posição mais baixa e os maiores as posições mais elevadas.

Reticulados (Lattices) §

Um reticulado, em termos matemáticos, é um conceito que se aplica a certos tipos de conjuntos parcialmente ordenados (c.p.o.). Em um reticulado, é possível realizar operações algébricas com seus elementos usando duas operações fundamentais: a operação de soma, denotada como (join em inglês), e a operação de produto, denotada como (meet em inglês). O é conhecido como o limitante superior e o como o limitante inferior.

A seguir os principais conceitos relacionados a reticulados:

1. Soma: A soma de dois elementos a e b em um c.p.o. é, se existir, o menor elemento que é maior ou igual a ambos, de acordo com a ordem parcial do c.p.o. Ou seja, é o elemento que “sucede” a e b na ordem do c.p.o.

2. Multiplicação: A multiplicação de dois elementos a e b, em um c.p.o. é, se existir, o maior elemento que é menor ou igual a ambos, de acordo com a ordem parcial do c.p.o. É o elemento que “antecede” a e b na ordem do c.p.o.

3. Reticulado: Um c.p.o. é considerado um reticulado quando qualquer par de elementos nesse c.p.o. pode ser submetido às operações de soma e multiplicação. Isso implica que todo par de elementos no reticulado tem tanto um limitante superior quanto um limitante inferior.

Referências §

---