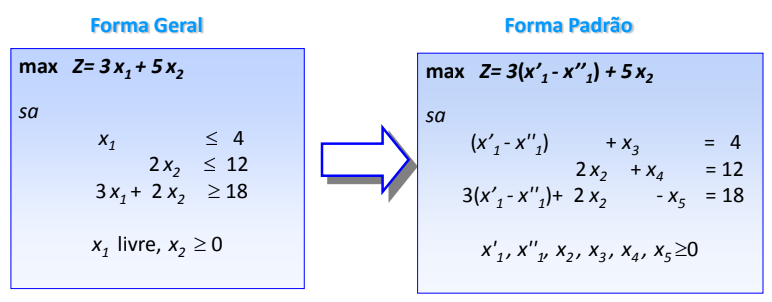
Redução à Forma Padrão

---

1. Transformações de maximização para minização

Qualquer problema de maximização pode ser convertido num problema de minimização, pois:

$$\text{min Z}=-\text{max(-Z)}$$

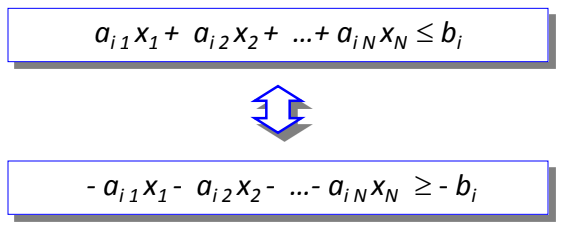
2. Transformação de $\le$ para $\ge$

Qualquer restrição de desigualdade de tipo "$\le$" pode ser convertida num restrição do tipo "$\ge$" multiplicando por $-1$ ambos os seus membros.

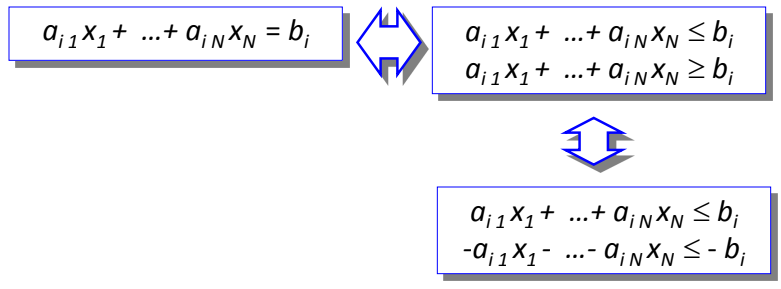
3. Transformações de igualdade em 2 de $\le$

Qualquer restrição de igualdade pode ser convertida em duas restrições de desigualdades "$\le$" equivalentes àquela.

O primeiro passo para a resolução de um problema de Programação Linear é a redução à Forma Padrão.

Para isto deve-se converter as restrições de desigualdade em equivalentes de igualdade.

Considerando uma desigualdade do tipo $\le$, podemos transformar em uma restrição de igualdade adicionando uma variável não negativa, chamada de variável de folga $x_{N-1}$.

Por outro lado, caso haja uma restrição de desigualdade de tipo $\ge$, podemos convertê-la em uma restrição de igualdade subtraindo uma variável não negativa, denominada de variável de excesso ou de folga $x_{N-1}$.

Exemplos:

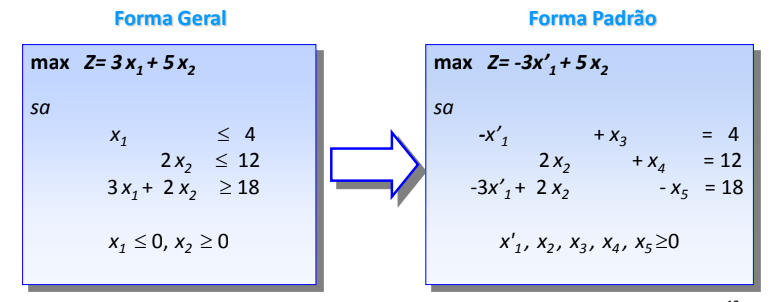
4. Transformação de variável negativa em não negativa

Qualquer variável negativa $x_j$, deve ser substituída por uma variável não negativa $x_j=-x_j^{{}^{\prime }}$, $x_j^{{}^{\prime }}\ge 0$, fazendo:

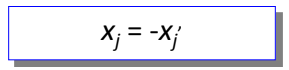
Exemplo:

5. Transformação de variável livre $x_j$

Para qualquer variável livre $x_j$, que não é restringida pela condição de não negatividade, pode ser substituída por um par de variáveis não negativas $x_j^{{}^{\prime }}\ge 0$ e $x_j^{{}^{\prime \prime }}\ge 0$, fazendo

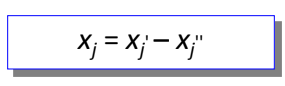
Desse modo, ao formularmos o problema novamente em função dessas duas variáveis, deletamos a variável $x_j$ do problema.

Exemplo:

Referências

---