Método da bissecção §

---

O Método da Bissecção é um dos métodos numéricos mais simples e intuitivos para encontrar soluções de equações não lineares da forma . Ele é um método iterativo que utiliza a propriedade de continuidade das funções e o Teorema do Valor Intermediário para localizar raízes dentro de um intervalo. O método é eficaz em encontrar a raiz, mas possui uma convergência lenta em comparação com outros métodos numéricos, como o Método de Newton.

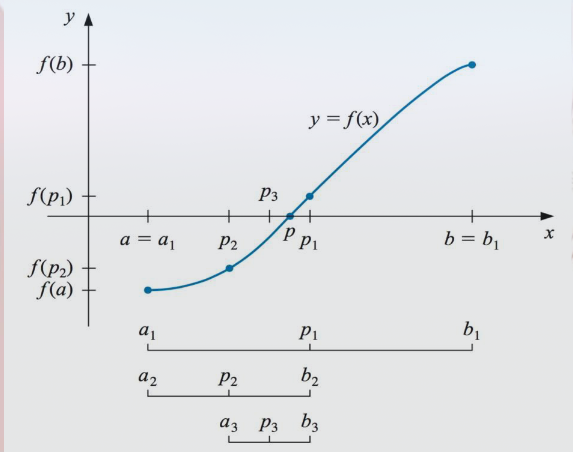
A ideia do Método da Bissecção é localizar uma raiz de uma função em um intervalo , onde é contínua, e aplicar sucessivas divisões desse intervalo para reduzir gradualmente a busca até encontrar a raiz com a precisão desejada.

O Teorema do Valor Intermediário nos diz que, se uma função é contínua em um intervalo fechado e e têm sinais opostos, isto é, , então existe pelo menos uma raiz no intervalo . A raiz é o valor onde a função cruza o eixo ().

Passos do Método de Bissecção §

1. Escolher um intervalo inicial , onde , ou seja, e têm sinais opostos, o que garante que há pelo menos uma raiz no intervalo.

2. Calcular o ponto médio do intervalo, ou seja, dividir o intervalo ao meio:

3. Verificar o sinal de :

   • Se , é a raiz exata e o processo termina.
   • Se não for zero, verificar o produto para determinar em qual metade do intervalo está a raiz:
     • Se , a raiz está no intervalo , então redefine-se .
     • Se , a raiz está no intervalo , então redefine-se .

4. Repetir o processo: O intervalo continua a ser subdividido ao meio iterativamente, recalculando o ponto médio e verificando o produto dos sinais até que a raiz seja localizada com a precisão desejada, ou seja, até que o intervalo seja suficientemente pequeno.

5. Critério de Parada: O método pode ser interrompido quando o tamanho do intervalo for menor que uma tolerância predefinida , indicando que a raiz foi localizada com precisão suficiente. Existem diversas maneira para critérios de parada.

Exemplo de Aplicação §

Vamos aplicar o Método da Bissecção para encontrar a raiz da função , que tem uma raiz em , no intervalo .

1. Escolha do intervalo: No intervalo ,

   Como , sabemos que há uma raiz no intervalo .

2. Primeira iteração:

   • O ponto médio é:
   • Calculando :
     Como , encontramos a raiz exata .

Neste caso, o método encontrou a raiz exata na primeira iteração, mas, em muitos casos, isso não acontece, e o método precisa continuar dividindo o intervalo até a raiz ser encontrada com a precisão desejada.

Convergência do Método §

O Método da Bissecção sempre converge, desde que a função seja contínua no intervalo e e tenham sinais opostos. A convergência, no entanto, é lenta, pois a cada iteração o tamanho do intervalo é reduzido pela metade. O número de iterações necessárias para garantir que o erro seja menor que uma tolerância pode ser estimado pela fórmula:

Isso indica que o número de iterações cresce logaritmicamente com o tamanho do intervalo inicial e com a precisão .

Referências §

---

Aula 4 - Método da bissecção