Método de Interpolação por Diferenças Divididas de Newton

---

O Método de Interpolação por Diferenças Divididas de Newton é uma técnica usada para construir um polinômio que passa por um conjunto de pontos conhecidos $(x_i,y_i)$.

Ele é eficiente e organizado, especialmente para adicionar novos pontos ao problema sem precisar refazer cálculos anteriores.

Ideia principal

A interpolação por diferenças divididas usa uma fórmula recursiva para calcular os coeficientes de um polinômio de Newton. Esses coeficientes são baseados em diferenças divididas entre os valores $y_i$ dos pontos, reduzindo o número de operações necessárias.

Fórmula do polinômio interpolador

O polinômio interpolador $P(x)$ no formato de Newton é dado por:

$$P(x)=f[x_0]+f[x_0,x_1](x-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1)+\cdots +f[x_0,x_1,\dots ,x_n](x-x_0)(x-x_1)\dots (x-x_{n-1}),$$

onde $f[x_0],f[x_0,x_1],f[x_0,x_1,x_2],\dots$ são as diferenças divididas (ou diferença dividida de ordem $n$).

Utilizando a notação de diferenças divididas, podemos reescrever o n-ésimo Polinômio de Lagrange $P_n(x)$ da seguinte fórmula:

$$P_n(x)=f[x_0]+\sum _{k=1}^{n}f[x_0,x_1,\dots ,x_k](x-x_0)\cdots (x-x_{k-1})$$

Sendo esta conhecida como a fórmula de Diferenças Divididas de Newton.

Diferenças divididas

As diferenças divididas são definidas recursivamente:

• Para um único ponto: $f[x_i]=y_i$.
• Para dois pontos: $f[x_i,x_j]=\frac{f[x_j]-f[x_i]}{x_j-x_i}$.
• Para mais pontos: $f[x_i,x_j,\dots ,x_k]=\frac{f[x_j,\dots ,x_k]-f[x_i,\dots ,x_{k-1}]}{x_k-x_i}$.

Esses valores representam as inclinações médias entre os pontos, capturando como a função muda.

Como aplicar o método

1. Identificar os pontos $(x_i,y_i)$: Liste os pontos conhecidos que o polinômio deve interpolar.

2. Montar a tabela de diferenças divididas: Calcule as diferenças divididas para os pontos dados.

3. Construir o polinômio $P(x)$: Substitua os coeficientes de diferenças divididas na fórmula de Newton.

   

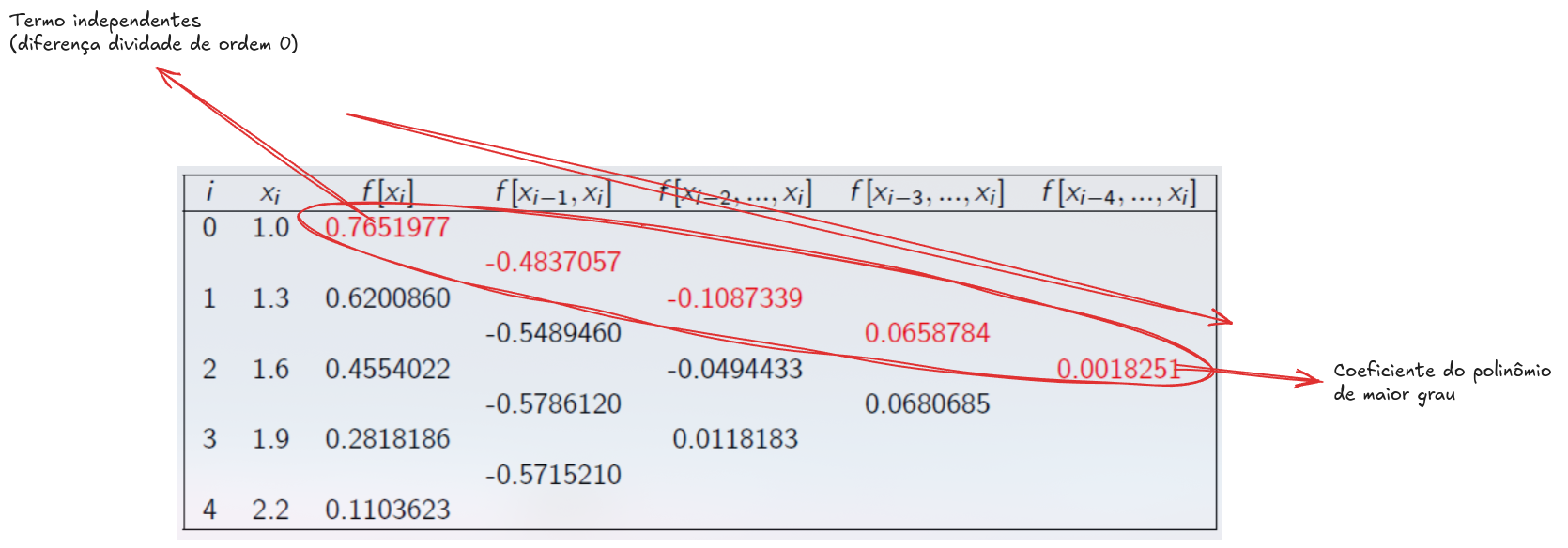
Exemplo prático:

Considere os pontos $(x_0,y_0)=(1,2)$, $(x_1,y_1)=(2,3)$, $(x_2,y_2)=(4,5)$.

1. Tabela de diferenças divididas:

   • $f[x_0]=2$, $f[x_1]=3$, $f[x_2]=5$.
   • $f[x_0,x_1]=\frac{3-2}{2-1}=1$, $f[x_1,x_2]=\frac{5-3}{4-2}=1$.
   • $f[x_0,x_1,x_2]=\frac{f[x_1,x_2]-f[x_0,x_1]}{4-1}=\frac{1-1}{3}=0$.

2. Polinômio interpolador:

   $$P(x)=f[x_0]+f[x_0,x_1](x-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1).$$

   Substituindo os valores:

   $$P(x)=2+1(x-1)+0(x-1)(x-2).$$

   Simplificando:

   $$P(x)=2+(x-1)=x+1.$$

---

Vantagens:

• Fácil de adicionar novos pontos ao polinômio sem refazer cálculos anteriores.
• Mais eficiente que outros métodos em problemas com muitos pontos.

Limitações:

• Pode ser menos intuitivo que o método de Lagrange.
• Se os pontos forem muito próximos, erros numéricos podem ocorrer em cálculos de diferenças divididas.

O método é uma ferramenta poderosa para interpolação e é amplamente utilizado em ciências e engenharia por sua flexibilidade e eficiência.

Referências

---

Aula 9 - Diferenças Divididas de Newton