Método de Newton
O Método de Newton, também conhecido como Método de Newton-Raphson, é uma técnica iterativa usada para encontrar aproximações para as raízes de uma equação .
Ele é amplamente utilizado devido à sua eficiência e rapidez, especialmente quando a solução inicial está próxima da raiz.
Como funciona:
A fórmula do método se baseia na ideia de aproximação linear:
Cite
A raiz da função é estimada pela interseção da reta tangente à curva de no ponto com o eixo .
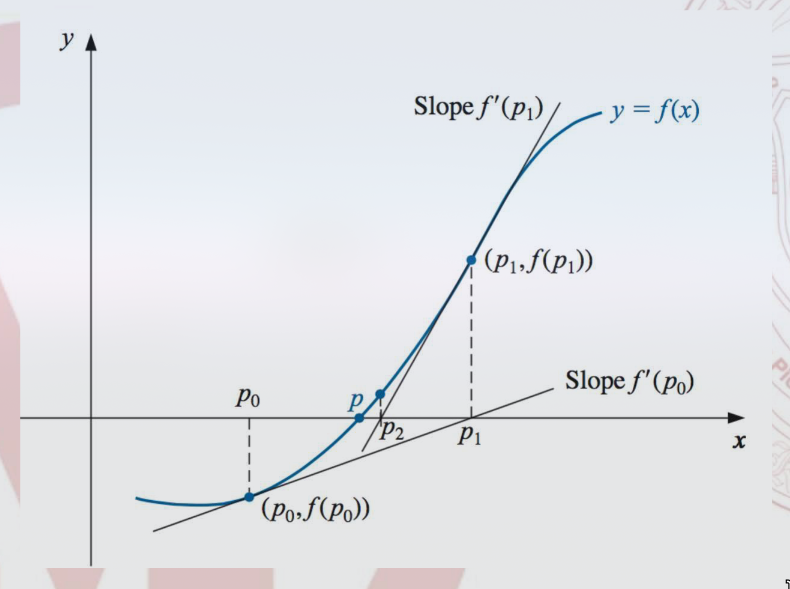
-
Ponto inicial: Escolhe-se um valor inicial , que é uma estimativa inicial da raiz.
-
Cálculo da próxima aproximação: A partir do valor inicial, calcula-se uma nova aproximação utilizando a fórmula:
Aqui, é a derivada da função .
-
Repetição: O processo é repetido até que a diferença entre as aproximações consecutivas seja suficientemente pequena, ou seja, até que a solução esteja dentro de um erro aceitável .
Critérios de paradas
Exemplo:
Imagine que queremos encontrar a raiz da função :
- Derivada: .
- Escolhemos um ponto inicial, como .
- Aplicamos a fórmula para calcular :
- Continuamos o processo para , até obter uma aproximação da raiz (neste caso, ).