Modelo de distribuição normal

---

Uma variável aleatória contínua tem distribuição normal se sua função de densidade de probabilidade é dada por:

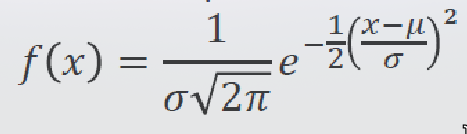
NOTE

A distribuição normal é a distribuição contínua mais utilizada na estatística.

Algumas características de uma distribuição considerada normal:

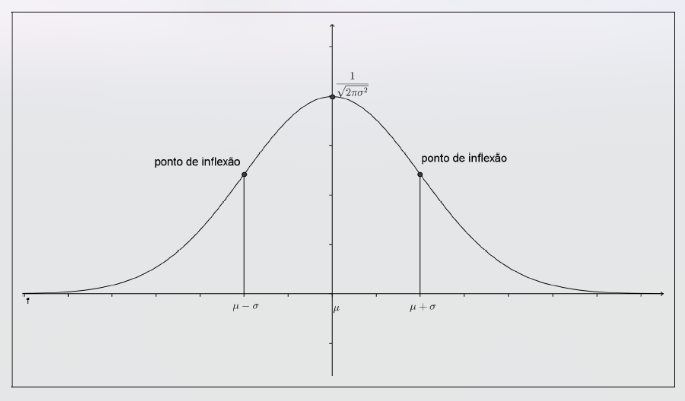
• $X=\mu$ é o ponto máximo de $f(x)$ → média
• $X=\mu +\sigma$ e $X=\mu -\sigma$ são os pontos de inflexão
• A curva é simétrica em relação a $\mu$ (média)
• $E(x)=\mu$ (média) e $var(x)=\sigma$ (desvio padrão)

NOTE

Um ponto de inflexão na distribuição normal refere-se a um ponto na curva de densidade de probabilidade onde a concavidade da função muda. Em outras palavras, é onde a curva passa de ser côncava para cima para ser côncava para baixo, ou vice-versa.

Para você calcular probabilidades normais, é necessário primeiro converter uma variável de uma distribuição normal $X$ (onde $XN(\mu ,\sigma )$), em uma variável aleatória normal padronizada $Z$ (onde $ZN(0,1)$, utilizando a seguinte fórmula de transformação.

$$Z=\frac{X-\mu }{\sigma }$$

NOTE

A variável $Z$ segue a distribuição normal padrão $N(0,1)$, que tem média 0 e desvio padrão 1

E a partir desse valor de Z, buscar na tabela de distribuição normal padronizada acumulada (em relação a média) para descubrir a probabilidade desse valor.

Referências

---

Aula 5 – Distribuição de Probabilidades –Modelos Contínuos