Notação Big O
A notação Big O, ou , é utilizada na análise de algoritmos para descrever um limite superior do crescimento de uma função à medida que o tamanho da entrada aumenta. Ela nos dá uma forma de quantificar como a complexidade de um algoritmo escala com o tamanho do problema, concentrando-se na taxa de crescimento da função no pior caso.
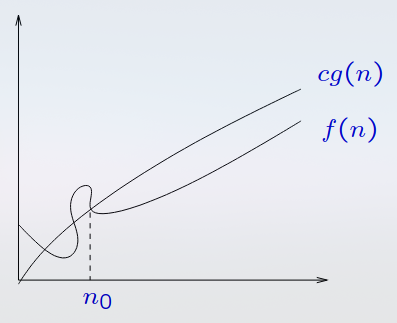
Definição Formal
Para uma função , o conjunto de funções é definido como:
Isso significa que, após um determinado valor , a função nunca cresce mais rápido que uma constante multiplicada por . Ou seja, delimita o crescimento de de forma assintótica.
Interpretação
A notação é usada para atribuir um limite superior para a função de complexidade. Em termos simples, se uma função está em , isso quer dizer que, para entradas grandes o suficiente, não cresce mais rápido que , até uma constante multiplicativa.
Exemplo 1: Verificar se
Aplicando a definição, queremos verificar se existe uma constante tal que:
Podemos reorganizar:
Tomando e , a desigualdade é verdadeira. Logo, podemos dizer que , o que significa que, para valores grandes de , a função cresce linearmente, assim como .
Exemplo 2: Verificar se
Agora, queremos verificar se para algum . Isso implicaria que:
No entanto, isso não é possível, pois cresce indefinidamente enquanto é uma constante. Portanto, , ou seja, cresce mais rápido que .