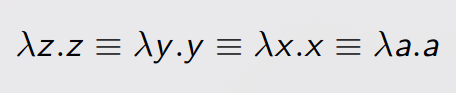Gramática do Cálculo Lambda §

---

A gramática do cálculo lambda é um conjunto de regras sintáticas que especifica como as expressões são formadas.

Uma expressão pode ser:

• Um nome (uma variável, como ou ),
• Uma função (uma abstração usando o símbolo ),
• Ou uma aplicação (a combinação de duas expressões).

Em notação formal, temos

Essas regras são o esqueleto do cálculo lambda e definem sua estrutura recursiva.

Nomes §

Um nome é simplesmente uma variável, como , ou . Ele representa um valor ou um “lugar reservado” que pode ser substituído mais tarde.

Pense nisso como as variáveis que você usa em álgebra ou programação, mas aqui, elas são puramente simbólicas, sem valores fixos até que sejam usadas em uma função ou aplicação.

Funções §

Uma função é definida como . Isso é chamado de abstração lambda e funciona assim:

• O símbolo indica que estamos criando uma função anônima.
• O após o é o parâmetro da função (a variável que será “ligada”).
• O ponto (.) separa o parâmetro do corpo da função, que é qualquer .

Por exemplo, é uma função que recebe e retorna — a chamada função identidade. É como dizer “faça nada além de devolver o que eu te dei”.

Aplicações §

Uma aplicação é escrita como , onde a primeira expressão é tipicamente uma função e a segunda é o argumento aplicado a ela.

Na prática, usamos parênteses para uma maior clareza, mas na gramática pura eles são implícitos.

Por exemplo, significa “aplique a função ao argumento ”. O resultado é , porque no corpo da função é substituído por .

Note

Esse processo de substituição é chamado de β-redução.

Exemplo §

Exemplo 1: Função identidade §

Considere a expressão:

Aqui, é a função identidade.

Warning

Os nomes dos argumentos nas definições de função não possuem nenhum significado.

Ou seja:

Para resolver, substituímos por no corpo da função, obtendo:

Note

Todas as ocorrências do identificador no corpo da definição são substituídos por .

Exemplo 2: Aplicação com duas variáveis §

A função é onde (argumento) consome (parâmetro).

Em outras palavras, substituímos por no corpo da função

O resultado é uma nova aplicação, , que pode ser interpretada dependendo do contexto (por exemplo, se fosse outra função).

Referências §

---

Aula 1 - Cálculo Lambda