Operador lógica AND no Cálculo Lambda §

---

Abstract

O operador lógico “E” (AND) é definido no cálculo lambda como , utilizando os booleanos de Church e .

No cálculo lambda, operações lógicas como o “E” (AND) são expressas como funções.

Já vimos que “verdadeiro” () e “falso” () são codificados como seletores de argumentos. Agora, vamos construir o operador “E” — que retorna “verdadeiro” apenas se ambos os operandos forem verdadeiros.

Definição §

O operador lógico “E” (AND) no cálculo lambda é definido como:

Onde:

• e são booleanos no cálculo lambda (ou seja, ou ),
• (escolhe o primeiro argumento),
• (escolhe o segundo argumento).

A expressão pode ser interpretada assim:

• é aplicado a e como argumentos.
• Se , então (escolhe ), e o resultado depende de .
• Se , então (escolhe ), e o resultado é sempre falso.

Isso captura a essência do “E”: o resultado é verdadeiro () apenas se ambos e forem verdadeiros.

Para transformar toda essa formalidade em forma mais visual e simples de interpretar isso e visualizar a função AND seria utilizando a tabela verdade abaixo:

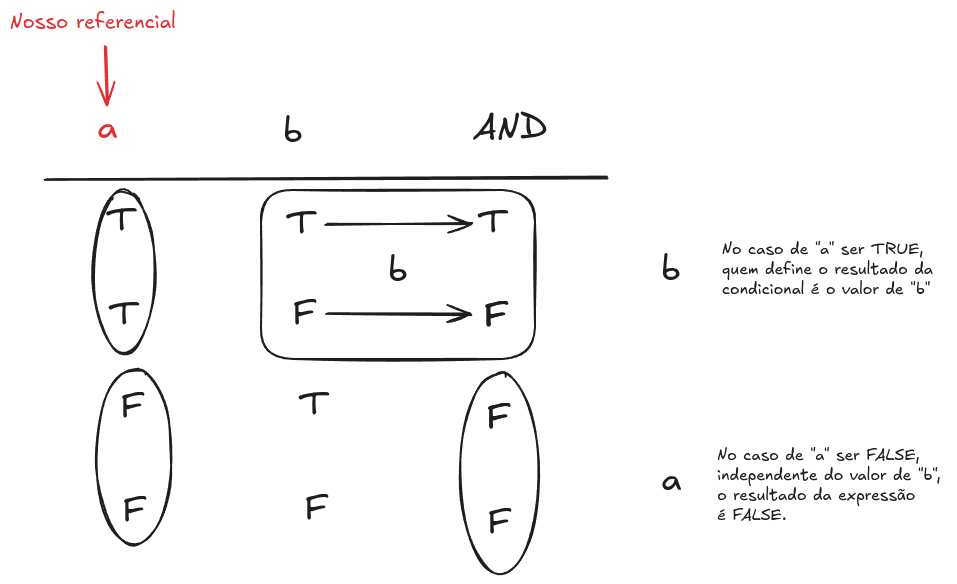Referência: Drawing 2025-03-03 10.40.11.excalidraw

Lemos essa imagem com a seguinte pergunta:

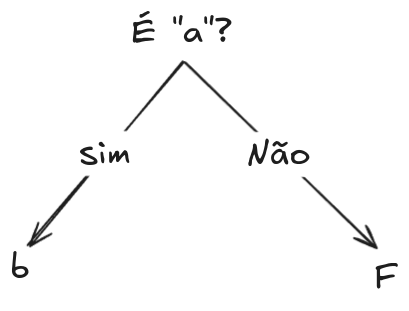
Visualizando operador AND na tabela verdade §

Para confirmar que corresponde ao operador “E” lógico, vamos calcular todas as combinações possíveis de e ( ou ) e comparar com a tabela verdade padrão.

Tabela verdade do “E” lógico:

Agora, vamos testar para cada caso.

Caso 1: , §

• Substituímos por :
• Substituímos por :
• Resultado: (verdadeiro).

Caso 2: , §

• Substituímos por :
• Substituímos por :
• Resultado: (falso).

Caso 3: , §

• Substituímos por :
• Substituímos por :
• Resultado: (falso).

Caso 4: , §

• Substituímos por :
• Substituímos por :
• Resultado: (falso).

Resultado final §

			Esperado ()

Referências §

---

Aula 1 - Cálculo Lambda